Next: The Matrix Representation of Up: Quantum Physics 130 Previous: 3D Symmetric HO in Contents
We have already solved many problems in Quantum Mechanics using wavefunctions and differential operators. Since the eigenfunctions of Hermitian operators are orthogonal (and we normalize them) we can now use the standard linear algebra to solve quantum problems with vectors and matrices. To include the spin of electrons and nuclei in our discussion of atomic energy levels, we will need the matrix representation.
These topics are covered at very different levels in Gasiorowicz Chapter 14, Griffiths Chapters 3, 4 and, more rigorously, in Cohen-Tannoudji et al. Chapters II, IV and IX.
System in a Magnetic Field*
*
System in a B-field
System in a B-field: Version I
in General Spin
State
for Spin
for Spin
State in a B field
Angular Momentum Operators*
![\bgroup\color{black}$[L_x,L_y]$\egroup](img1036.png)
Using Matrices *
*
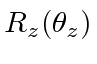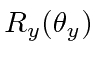Rotation Operator
*
Rotation Operator
*
Operators
Rotation Matrices *