Next: Eigenvectors of for Spin Up: Examples Previous: Expectation of in General Contents
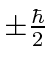 .
So, factoring out the constant, we have
.
So, factoring out the constant, we have
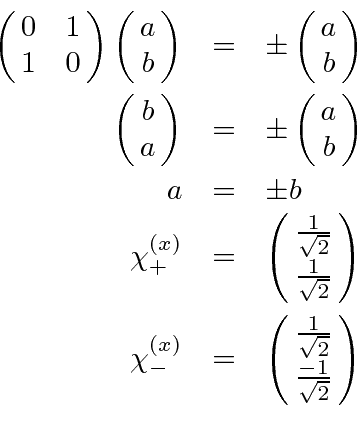
The remainder of this section goes into more detail on this calculation but is currently notationally challenged.
Recall the standard method of finding eigenvectors and eigenvalues:
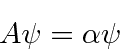
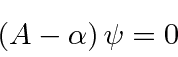

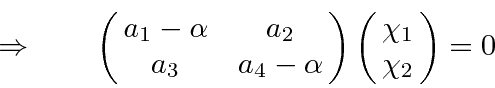
For a matrix times a nonzero vector to give zero, the determinant of the
matrix must be zero.
This gives the ``characteristic
equation'' which for spin
![]() systems will be a quadratic equation in
the eigenvalue
systems will be a quadratic equation in
the eigenvalue
![]() :
:
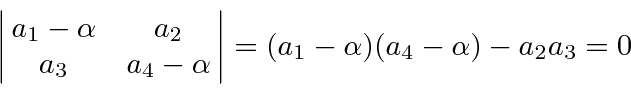
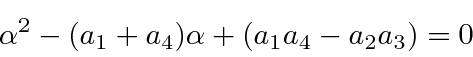
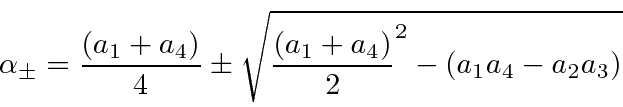
To find the eigenvectors, we simply replace (one at a time) each of the
eigenvalues above into the equation
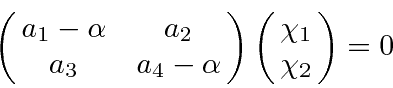
Now specifically, for the operator
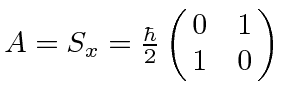 , the eigenvalue equation
, the eigenvalue equation
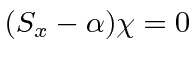 becomes, in
matrix notation,
becomes, in
matrix notation,
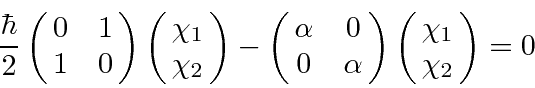
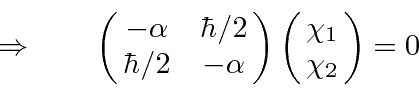
The characteristic equation is
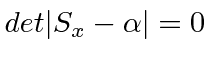 , or
, or
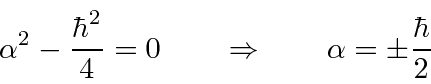
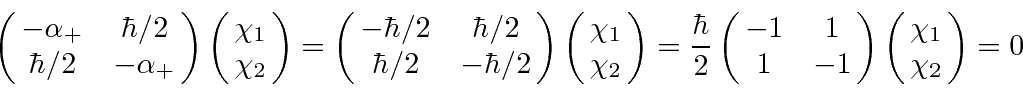
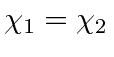 (just write out the
two component equations to see this). Hence the normalized eigenvector
corresponding to the eigenvalue
(just write out the
two component equations to see this). Hence the normalized eigenvector
corresponding to the eigenvalue
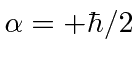 is
is
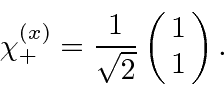
Similarly, we find for the eigenvalue
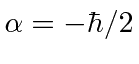 ,
,
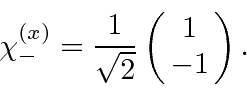
Jim Branson 2013-04-22