Next: Harmonic Oscillator Lowering Operator Up: Examples Previous: Harmonic Oscillator Hamiltonian Matrix Contents
We wish to find the matrix representing the 1D harmonic oscillator raising operator.
We use the
raising operator
equation for an energy eigenstate.
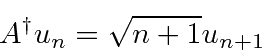
Now simply compute the matrix element.
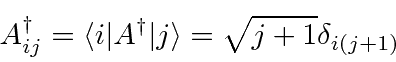
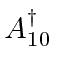 in the second row and first column.
All he entries will be on a diagonal from that one.
in the second row and first column.
All he entries will be on a diagonal from that one.

Jim Branson 2013-04-22