Next: Introducing and Up: Quantum Physics 130 Previous: Sample Test Problems Contents
Operator methods are very useful both for solving the Harmonic Oscillator problem and for any type of computation for the HO potential. The operators we develop will also be useful in quantizing the electromagnetic field.
The Hamiltonian for the 1D Harmonic Oscillator
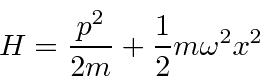
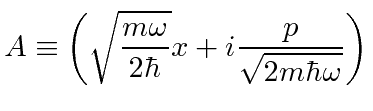 |
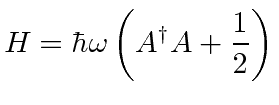 |
We will use the
commutators
between
![]() ,
,
![]() and
and
![]() to solve the HO problem.
to solve the HO problem.
![\bgroup\color{black}$\displaystyle [A,A^\dagger]=1 $\egroup](img1428.png) |
![\begin{eqnarray*}[H,A]&=&-\hbar\omega A \\
{[H,A^\dagger]}&=&\hbar\omega A^\dagger \\
\end{eqnarray*}](img1429.png)
From these commutators we can show that
![]() is a
raising operator
for Harmonic Oscillator states
is a
raising operator
for Harmonic Oscillator states
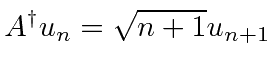 |
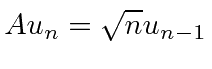 |
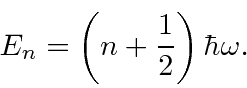
The
actual wavefunctions
can be deduced by using the differential operators for
![]() and
and
![]() , but
often it is more useful to define the
, but
often it is more useful to define the
![]() eigenstate in terms of the ground state and raising operators.
eigenstate in terms of the ground state and raising operators.
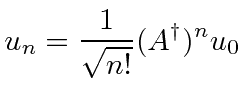 |
Almost any calculation of interest can be done without actual functions since we can express the operators for position and momentum.
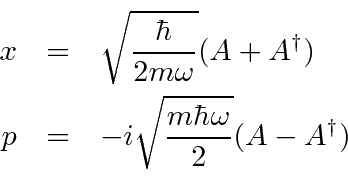
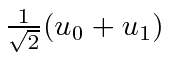 .
.
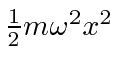 in eigenstate
in eigenstate
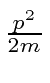 in eigenstate
in eigenstate