The Wavefunction for the HO Ground State

The equation

$$\bgroup\color{black} Au_0=0 \egroup$$

can be used to find the ground state wavefunction. Write $A$ in terms of $x$ and $p$ and try it.

$$\begin{eqnarray*} \left(\sqrt{m\omega\over 2\hbar}x+i{p\over\sqrt{2m\hbar\omega}... ...dx}\right)u_0=0 \\ {du_0\over dx}=-{m\omega x\over\hbar}u_0 \\ \end{eqnarray*}$$

This first order differential equation can be solved to get the wavefunction.

$$\bgroup\color{black} u_0=Ce^{-m\omega x^2/2\hbar} .\egroup$$

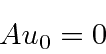
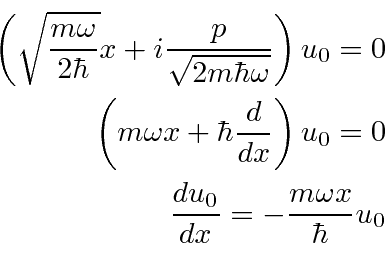
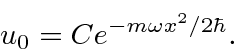
We could continue with the raising operator to get excited states.

$$\bgroup\color{black} \sqrt{1}u_1=\left(\sqrt{m\omega\over 2\hbar}x-\sqrt{\hbar\over 2m\omega}{d\over dx}\right)u_0 \egroup$$

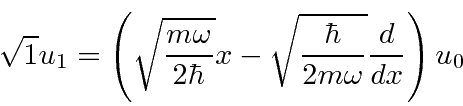
Usually we will not need the actual wave functions for our calculations.