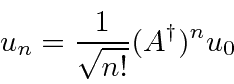Raising and Lowering Constants

We know that $A^\dagger$ raises the energy of an eigenstate but we do not know what coefficient it produces in front of the new state.

$$\bgroup\color{black} A^\dagger u_n=Cu_{n+1} \egroup$$

We can compute the coefficient using our operators.

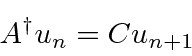
$$\begin{eqnarray*} \vert C\vert^2 &=&\langle A^\dagger u_n\vert A^\dagger u_n\ran... ...]) u_n\vert u_n\rangle= (n+1)\langle u_n\vert u_n\rangle=n+1 \\ \end{eqnarray*}$$

The effect of the raising operator is

$$\bgroup\color{black}A^\dagger u_n=\sqrt{n+1}u_{n+1}.\egroup$$

Similarly, the effect of the lowering operator is

$$\bgroup\color{black} Au_n=\sqrt{n}u_{n-1} .\egroup$$

These are extremely important equations for any computation in the HO problem.

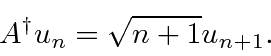
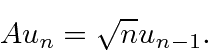
We can also write any energy eigenstate in terms of the ground state and the raising operator.

$$\bgroup\color{black} u_n={1\over\sqrt{n!}}(A^\dagger)^nu_0 \egroup$$