- A 1D harmonic oscillator is in a linear combination of the energy eigenstates
Find the expected value of 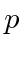 .
.
Answer
- Assuming
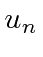 represents the
represents the 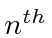 1D harmonic oscillator energy eigenstate,
calculate
1D harmonic oscillator energy eigenstate,
calculate
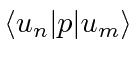 .
.
Answer
- Evaluate the ``uncertainty'' in
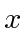 for the 1D HO ground state
for the 1D HO ground state
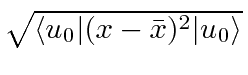 where
where
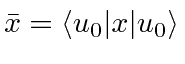 .
Similarly, evaluate the uncertainty in
.
Similarly, evaluate the uncertainty in 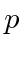 for the ground state.
What is the product
for the ground state.
What is the product
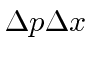 ?
?
Answer
Its easy to see that 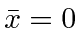 either from the integral or using operators.
I'll use operators to compute the rest.
either from the integral or using operators.
I'll use operators to compute the rest.
- Use the commutator relation between
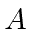 and
and 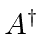 to derive
to derive ![$[H,A]$](img1494.png) .
Now show that
.
Now show that 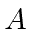 is the lowering operator for the harmonic oscillator energy.
is the lowering operator for the harmonic oscillator energy.
- At
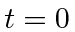 , a one dimensional harmonic oscillator is in the state
, a one dimensional harmonic oscillator is in the state
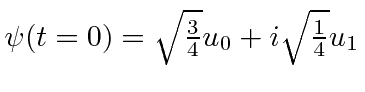 .
Calculate the expected value of
.
Calculate the expected value of  as a function of time.
as a function of time.
- At
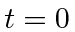 , a harmonic oscillator is in a linear combination of the
, a harmonic oscillator is in a linear combination of the 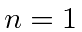 and
and 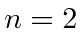 states.
states.
Find
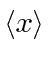 and
and
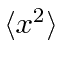 as a function of time.
as a function of time.
- A 1D harmonic oscillator is in a linear combination of the energy eigenstates
Find
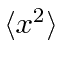 .
.
Jim Branson
2013-04-22
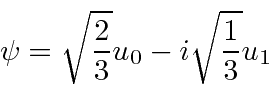
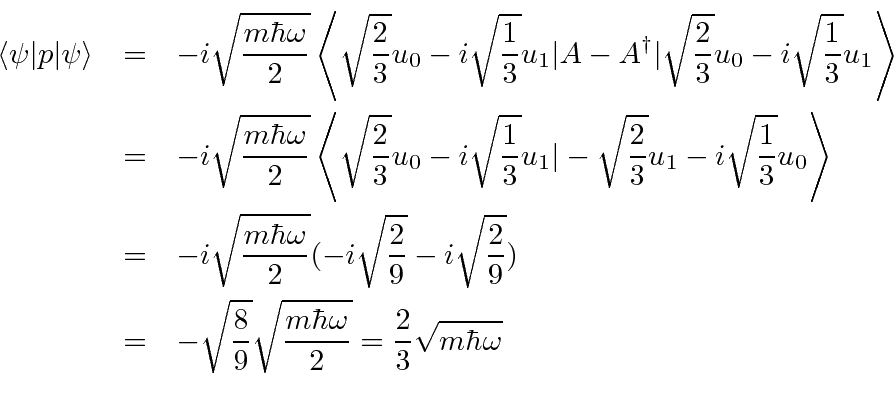
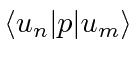 .
.
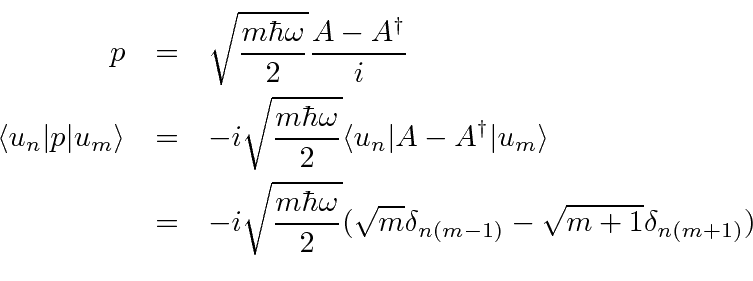
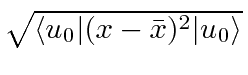 where
where
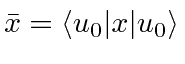 .
Similarly, evaluate the uncertainty in
.
Similarly, evaluate the uncertainty in 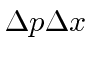 ?
?
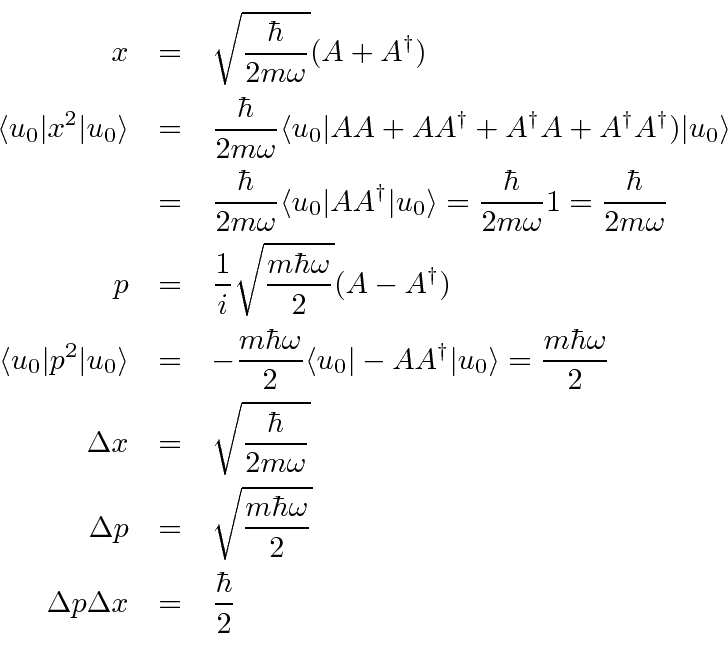
![$[H,A]$](img1494.png) .
Now show that
.
Now show that 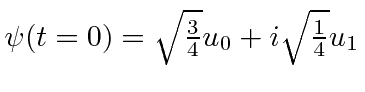 .
Calculate the expected value of
.
Calculate the expected value of 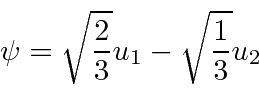
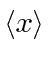 and
and
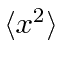 as a function of time.
as a function of time.
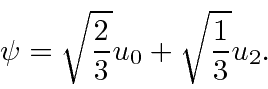
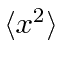 .
.