Rotation operators for $\ell=1$ *

We have chosen the $z$ axis arbitrarily. We could choose any other direction to define our basis states. We wish to know how to transform from one coordinate system to another. Experience has shown that knowing how an object transforms under rotations is important in classifying the object: scalars, vectors, tensors...

We can derive the operator for rotations about the z-axis. This operator transforms an angular momentum state vector into an angular momentum state vector in the rotated system.

$$\begin{eqnarray*} R_z(\theta_z)&=&e^{i\theta_zL_z/\hbar} \\ \psi'&=&R_z(\theta_z)\psi \end{eqnarray*}$$

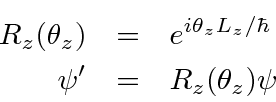
Since there is nothing special about the z-axis, rotations about the other axes follow the same form.

$$\begin{eqnarray*} R_x(\theta_x)&=&e^{i\theta_xL_x/\hbar} \\ R_y(\theta_y)&=&e^{i\theta_yL_y/\hbar} \end{eqnarray*}$$

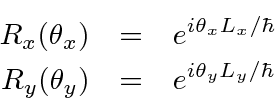
The above formulas for the rotation operators must apply in both the matrix representation and in the differential operator representation.

Redefining the coordinate axes cannot change any scalars, like dot products of state vectors. Operators which preserve dot products are called unitary. We proved that operators of the above form, (with hermitian matrices in the exponent) are unitary.

A computation of the operator for rotations about the z-axis gives

$$\bgroup\color{black}R_z(\theta_z)=\left(\matrix{e^{i\theta_z}&0&0\cr 0&1&0\cr 0&0&e^{-i\theta_z}}\right).\egroup$$

A computation of the operator for rotations about the y-axis yields

$$\bgroup\color{black}R_y(\theta_y)=\left(\matrix{ {1\over 2}(... ...2}}\sin(\theta_y)&{1\over 2}(1+\cos(\theta_y)) }\right).\egroup$$

Try calculating the rotation operator for the x-axis yourself.

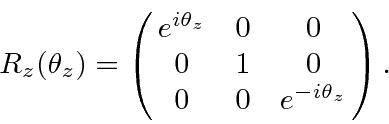
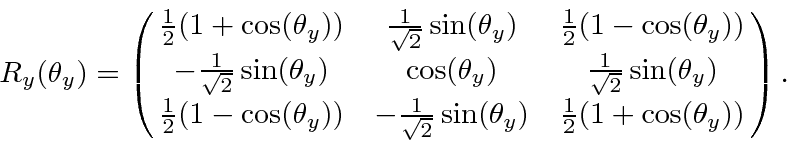
Note that both of the above rotation matrices reduce to the identity matrix for rotations of $2\pi$ radians. For a rotation of $\pi$ radians, $R_y$ interchanges the plus and minus components (and changes the sign of the zero component), which is consistent with what we expect. Note also that the above rotation matrices are quite different than the ones used to transform vectors and tensors in normal Euclidean space. Hence, the states here are of a new type and are referred to as spinors.

* Example: A 90 degree rotation about the z axis.*