Next: Derive Spin Operators Up: Derivations and Computations Previous: Compute the Rotation Operator Contents
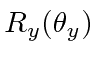 *
*
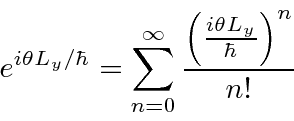
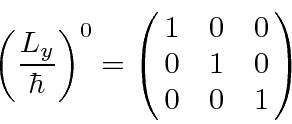
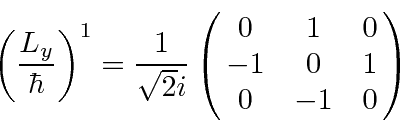
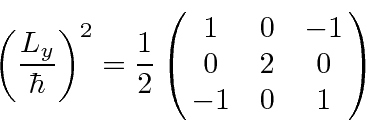
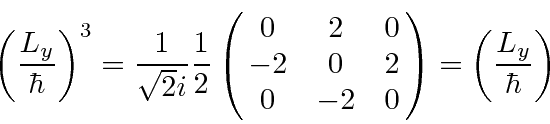
All the odd powers are the same. All the nonzero even powers are the same.
The
![]() s all cancel out.
We now must look at the sums for each term in the matrix and identify the function it
represents.
s all cancel out.
We now must look at the sums for each term in the matrix and identify the function it
represents.
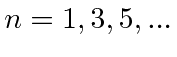 terms sum to
terms sum to
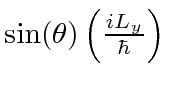 .
.
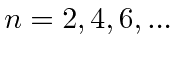 terms (with a -1 in the matrix) are nearly the series for
terms (with a -1 in the matrix) are nearly the series for
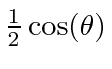 .
The
.
The
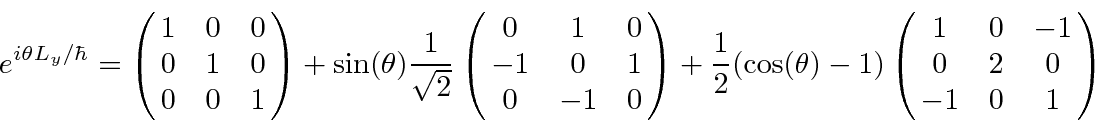
Putting this all together, we get
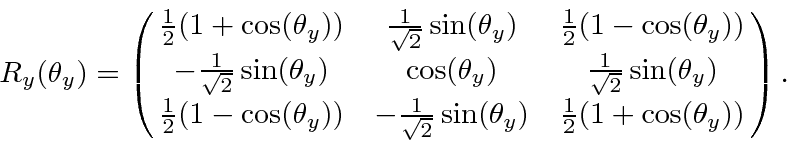
Jim Branson 2013-04-22