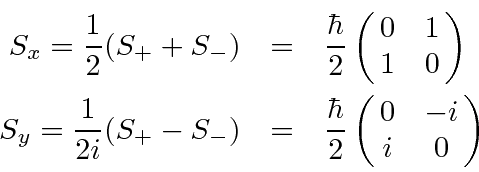Derive Spin
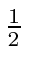 Operators
Operators
We will again use eigenstates of
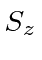 , as the basis states.
, as the basis states.
Its easy to see that this is the only matrix that works.
It must be diagonal since the basis states are eigenvectors of the matrix.
The correct eigenvalues appear on the diagonal.
Now we do the raising and lowering operators.
We can now calculate
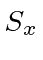 and
and
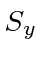 .
.
These are again Hermitian, Traceless matrices.
Jim Branson
2013-04-22
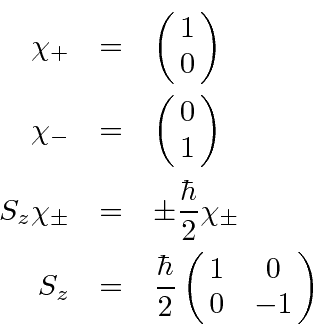
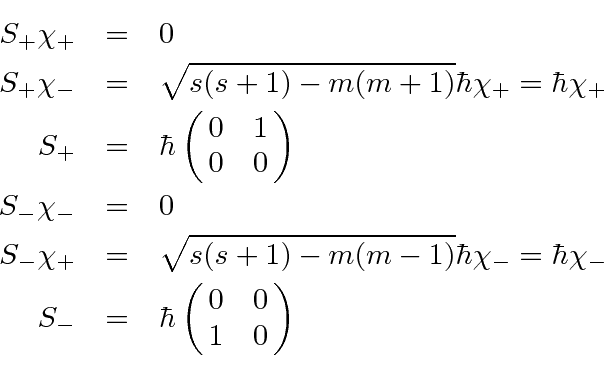
![]() and
and
![]() .
.