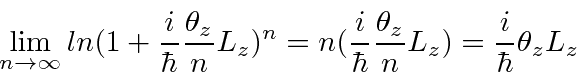Derive the Expression for Rotation Operator
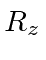 *
*
The laws of physics do not depend on what axes we choose for our coordinate system-
There is rotational symmetry.
If we make an infinitesimal rotation (through and angle
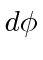 )
about the z-axis, we get the transformed coordinates
)
about the z-axis, we get the transformed coordinates
We can Taylor expand any function
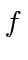 ,
,
So the rotation operator for the function is
A finite rotation can be made by applying the operator for an infinitesimal rotation over and over.
Let
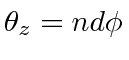 . Then
. Then
The last step, converting the limit to an exponential is a known identity.
We can verify it by using the log of the quantity.
First we expand
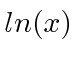 about
about
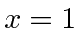 :
:
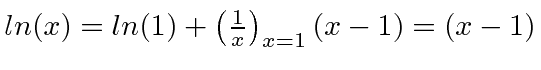 .
.
So exponentiating, we get the identity.
Jim Branson
2013-04-22
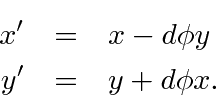
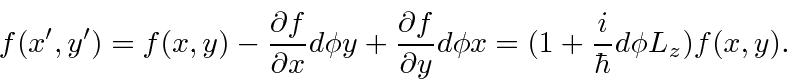
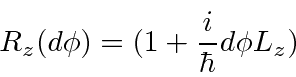
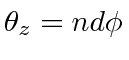 . Then
. Then
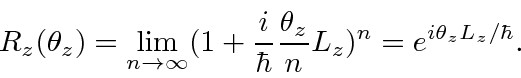
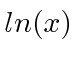 about
about
![]() :
:
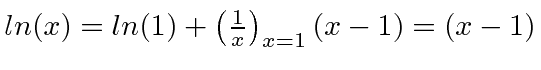 .
.