Next: Spin Up: Operators Matrices and Spin Previous: Rotation operators for * Contents
Imagine a Stern-Gerlach apparatus that first separates an
![]() atomic beam
with a strong B-field gradient in the z-direction.
Let's assume the beam has atoms moving in the y-direction.
The apparatus blocks two separated beams, leaving only the eigenstate of
atomic beam
with a strong B-field gradient in the z-direction.
Let's assume the beam has atoms moving in the y-direction.
The apparatus blocks two separated beams, leaving only the eigenstate of
![]() with eigenvalue
with eigenvalue
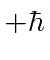 .
We follow this with an apparatus which separates in the u-direction, which is at
an angle
.
We follow this with an apparatus which separates in the u-direction, which is at
an angle
![]() from the z-direction, but still perpendicular to the direction of
travel of the beam, y.
What fraction of the (remaining) beam will go into each of the three beams which are
split in the u-direction?
from the z-direction, but still perpendicular to the direction of
travel of the beam, y.
What fraction of the (remaining) beam will go into each of the three beams which are
split in the u-direction?
We could represent this problem with the following diagram.
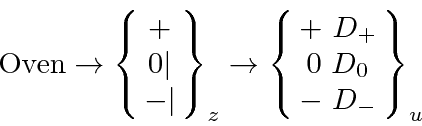
To solve this with the rotation matrices, we first determine the state after the first
apparatus. It is just
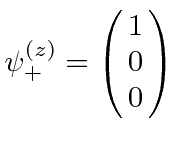 with the usual basis.
Now we rotate to a new (primed) set of basis states with the
with the usual basis.
Now we rotate to a new (primed) set of basis states with the
![]() along the
along the
![]() direction.
This means a rotation through an angle
direction.
This means a rotation through an angle
![]() about the y direction.
The problem didn't clearly define whether it is
about the y direction.
The problem didn't clearly define whether it is
![]() or
or
![]() , but, if we only
need to know the intensities, it doesn't matter.
So the state coming out of the second apparatus is
, but, if we only
need to know the intensities, it doesn't matter.
So the state coming out of the second apparatus is
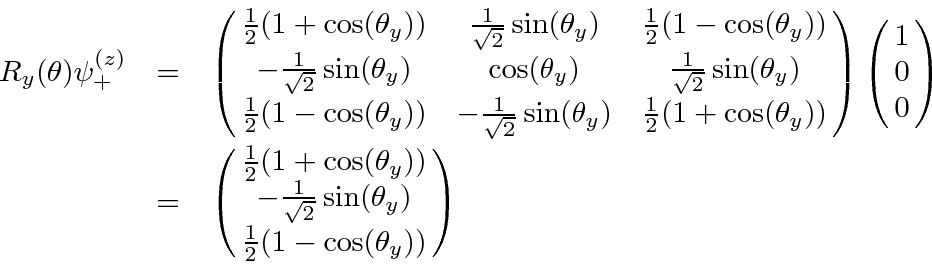
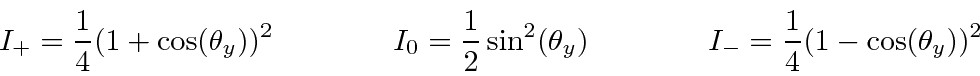
An alternate solution would be to use the
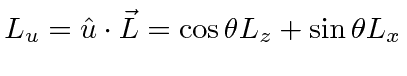 operator. Find the eigenvectors of this operator, like
operator. Find the eigenvectors of this operator, like
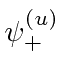 . The intensity in the +
beam is then
. The intensity in the +
beam is then
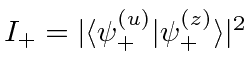 .
.
Jim Branson 2013-04-22