Next: Other Two State Systems* Up: Operators Matrices and Spin Previous: A Rotated Stern-Gerlach Apparatus* Contents
Earlier, we showed that both integer and half integer angular momentum could satisfy the commutation relations for angular momentum operators but that there is no single valued functional representation for the half integer type.
Some particles, like electrons, neutrinos, and quarks
have half integer internal angular momentum, also called spin.
We will now develop a spinor representation for spin
![]() .
There are no coordinates
.
There are no coordinates
![]() and
and
![]() associated with internal angular momentum so the
only thing we have is our spinor representation.
associated with internal angular momentum so the
only thing we have is our spinor representation.
Electrons, for example, have total spin one half.
There are no spin 3/2 electrons so there are only two possible spin states for an electron.
The usual basis states are the eigenstates of
![]() .
We know from our study of angular momentum,
that the eigenvalues of
.
We know from our study of angular momentum,
that the eigenvalues of
![]() are
are
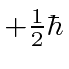 and
and
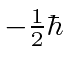 .
We will simply represent the
.
We will simply represent the
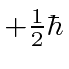 eigenstate as the upper component of a 2-component vector.
The
eigenstate as the upper component of a 2-component vector.
The
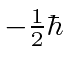 eigenstate amplitude is in the lower component.
So the pure eigenstates are.
eigenstate amplitude is in the lower component.
So the pure eigenstates are.
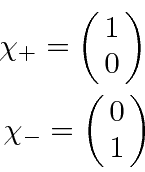
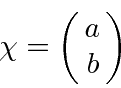
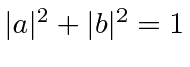 .
.
It is easy to
derive
the matrix operators for spin.
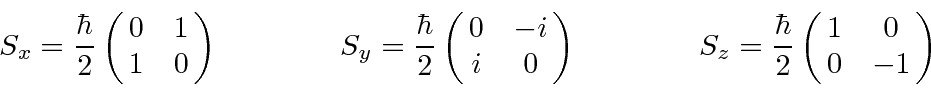
![\begin{eqnarray*}[S_x,S_y]&=&{\hbar^2\over 4} \left[\pmatrix{0 &1\cr 1 &0\cr}\pm...
...i\cr}=i\hbar {\hbar\over 2}\pmatrix{1 &0\cr 0 &-1\cr}=i\hbar S_z
\end{eqnarray*}](img2200.png)
The spin operators are an (axial) vector of matrices.
To form the spin operator for an arbitrary direction
![]() , we simply dot the unit vector into the vector of matrices.
, we simply dot the unit vector into the vector of matrices.
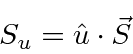
The Pauli Spin Matrices,
![]() , are simply defined and have the following properties.
, are simply defined and have the following properties.
![\begin{eqnarray*}
S_i &\equiv & {\hbar\over 2} \sigma_i \\
\vec{S}&=&{\hbar\ove...
...sigma_j\right] & = & 2i\epsilon_{ijk}\sigma_k \\
\sigma_i^2&=&1
\end{eqnarray*}](img2203.png)
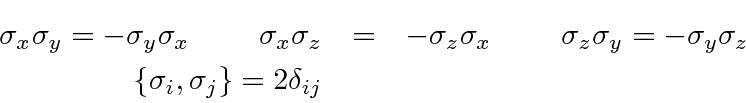
* Example:
The expectation value of ![]() .*
.*
* Example:
The eigenvectors of ![]() .*
.*
* Example:
The eigenvectors of ![]() .*
.*
The (passive) rotation operators, for rotations of the coordinate axes can be
computed
from the formula
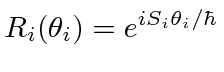 .
.
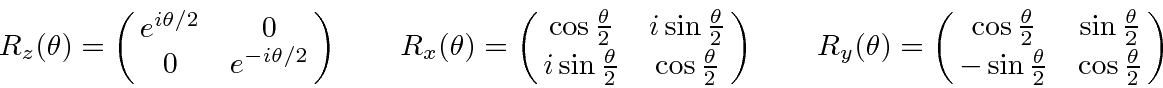
* Example:
The eigenvectors of ![]() .*
.*
As for orbital angular momentum (
![]() ), there is also a magnetic moment associated with
internal angular momentum (
), there is also a magnetic moment associated with
internal angular momentum (
![]() ).
).
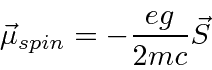
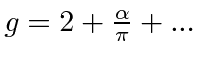 .
For particles with structure, like the proton or neutron,
.
For particles with structure, like the proton or neutron,
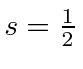 ,
the magnetic moment due to the spin of an electron is almost exactly equal to the magnetic
moment due to the orbital angular momentum in an
,
the magnetic moment due to the spin of an electron is almost exactly equal to the magnetic
moment due to the orbital angular momentum in an
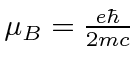 .
.
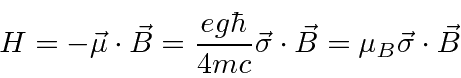
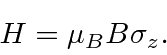
A beam of spin one-half particles can also be separated by a Stern-Gerlach apparatus which uses a large gradient in the magnetic field to exert a force on particles proprtional to the component of spin along the field gradient. Thus, we can measure the component of spin along a direction we choose. A field gradient will separate a beam of spin one-half particles into two beams. The particles in each of those beams will be in a definite spin state, the eigenstate with the component of spin along the field gradient direction either up or down, depending on which beam the particle is in.
We may represent a Stern-Gerlach appartatus which blocks the lower beam by the symbol below.
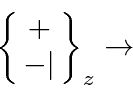
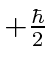 eigenstate.
eigenstate.
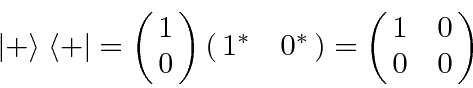
We can perform several thought experiments.
The appartus below starts with an unpolarized beam.
In such a beam we don't know the state of any of the particles.
For a really unpolarized beam, half of the particles will go into each of the separated beams.
(Note that an unpolarized beam cannot be simply represented by a state vector.)
In the apparatus below, we block the upper beam so that only half of the particles come out of the first part of the
apparatus and all of those particles are in the definite state having spin down along the z axis.
The second part of the apparatus blocks the lower separated beam.
All of the particles are in the lower beam so nothing is left coming out of the apparatus.
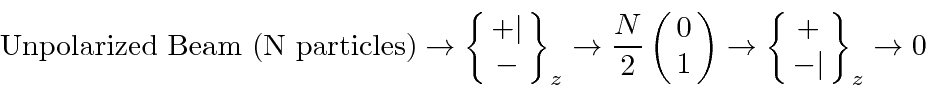
The result is unaffected if we insert an additional apparatus that separates in the x direction in the middle of the
apparatus above.
While the apparatus separates, neither beam is blocked (and we assume we cannot observe which particles go into which beam).
This apparatus does not change the state of the beam!
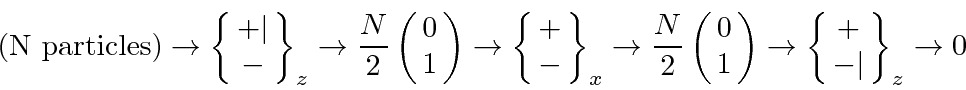
Now if we block one of the beams separated according to the x direction, particles can get through the whole apparatus.
The middle part of the apparatus projects the state onto the positive eigenstate of
![]() .
This state has equal amplitudes to have spin up and spin down along the z direction.
So now, 1/8 of the particles come out of the apparatus.
By blocking one beam, the number of particles coming out increased from 0 to
.
This state has equal amplitudes to have spin up and spin down along the z direction.
So now, 1/8 of the particles come out of the apparatus.
By blocking one beam, the number of particles coming out increased from 0 to
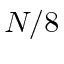 .
This seems a bit strange but the simple explanation is that the upper and lower beams of the middle part of the apparatus
were interfering to give zero particles.
With one beam blocked, the inteference is gone.
.
This seems a bit strange but the simple explanation is that the upper and lower beams of the middle part of the apparatus
were interfering to give zero particles.
With one beam blocked, the inteference is gone.
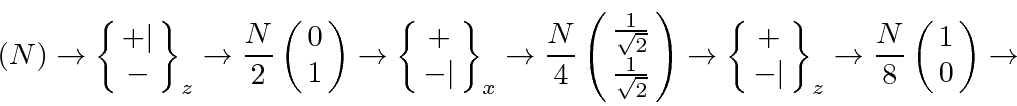
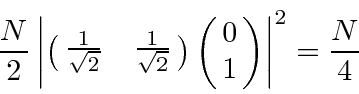
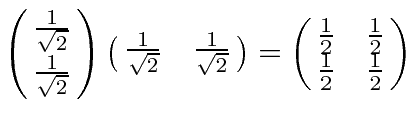 .
.
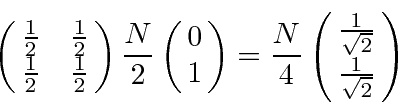
Jim Branson 2013-04-22