Next: Examples Up: Derivations and Computations Previous: Spherical Coordinates and the Contents
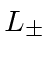
The next step is to figure out how the
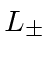 operators change the eigenstate
operators change the eigenstate
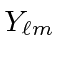 .
What eigenstates of
.
What eigenstates of
![]() are generated when we operate with
are generated when we operate with
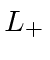 or
or
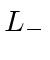 ?
?
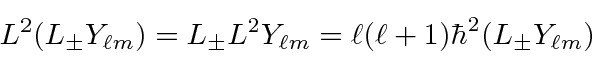
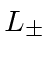 , we see that we have the same
, we see that we have the same
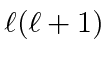 after operation.
This is also true for operations with
after operation.
This is also true for operations with
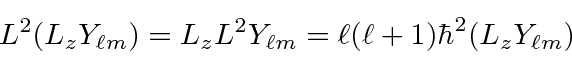
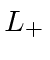 ,
,
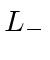 and
and
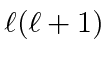 .
.
The eigenvalue of
![]() is changed when we operate with
is changed when we operate with
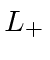 or
or
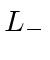 .
.
![\begin{eqnarray*}
L_z(L_\pm Y_{\ell m})&=&L_\pm L_z Y_{\ell m}+[L_z,L_\pm]Y_{\e...
...pm\hbar L_\pm Y_{\ell m}
=(m\pm 1)\hbar (L_\pm Y_{\ell m}) \\
\end{eqnarray*}](img1778.png)
From the above equation we can see that
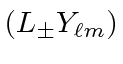 is an eigenstate of
is an eigenstate of
![]() .
.
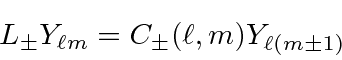
Since
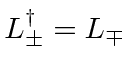 , its easy to show that the following is greater than zero.
, its easy to show that the following is greater than zero.
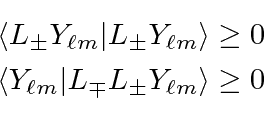
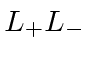 in terms of our chosen operators,
in terms of our chosen operators,
![\begin{eqnarray*}
L_\mp L_\pm&=&(L_x\mp iL_y)(L_x\pm iL_y)=L_x^2+L_y^2\pm iL_xL...
..._x \\
&=&L_x^2+L_y^2\pm i[L_x,L_y]=L^2-L_z^2\mp\hbar L_z \\
\end{eqnarray*}](img1784.png)
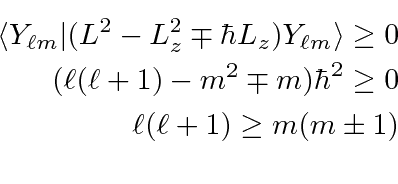
We know that the eigenvalue
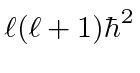 is greater than zero.
We can assume that
is greater than zero.
We can assume that
 .
.
The condition that
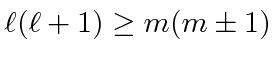 then becomes a limit on
then becomes a limit on
![]() .
.
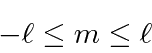
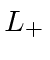 raises
raises
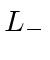 lowers
lowers
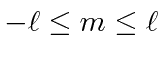 , the raising and lowering must stop
for
, the raising and lowering must stop
for
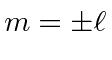 ,
,
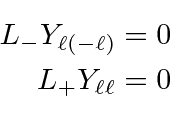
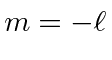 ,
there will be states in integer steps up to
,
there will be states in integer steps up to
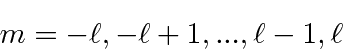
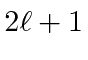 states with the same
states with the same
The eigenstates of
![]() and
and
![]() should be normalized
should be normalized
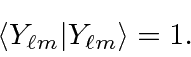
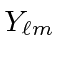 give
give
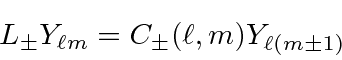
The coefficient
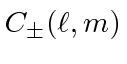 can be computed.
can be computed.
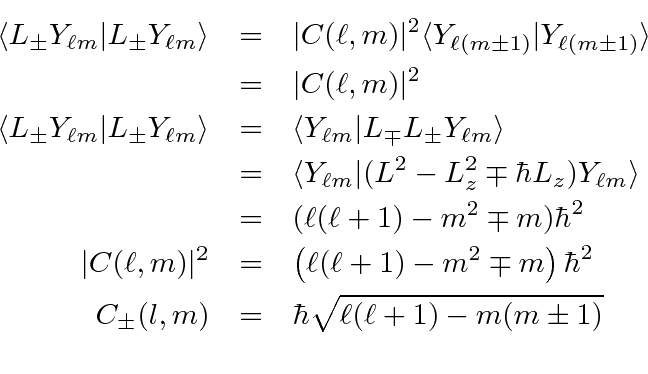
We now have the effect of the raising and lowering operators in terms of the normalized
eigenstates.
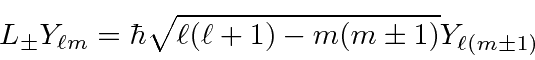
Jim Branson 2013-04-22