Next: Derivations and Computations Up: Examples Previous: Time Development of a Contents
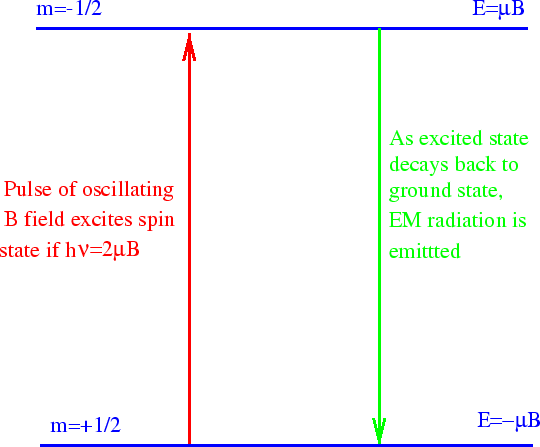
In basic NMR, a strong static B field is applied. A spin
![]() proton in a hydrogen nucleus
then has two energy eigenstates. After some time, most of the protons fall into the lower of the
two states. We now use an electromagnetic wave (RF pulse) to excite some of the protons back
into the higher energy state.
Surprisingly, we can calculate this process already.
The proton's magnetic moment interacts with the oscillating B field of the EM wave.
proton in a hydrogen nucleus
then has two energy eigenstates. After some time, most of the protons fall into the lower of the
two states. We now use an electromagnetic wave (RF pulse) to excite some of the protons back
into the higher energy state.
Surprisingly, we can calculate this process already.
The proton's magnetic moment interacts with the oscillating B field of the EM wave.
As we derived, the Hamiltonian is
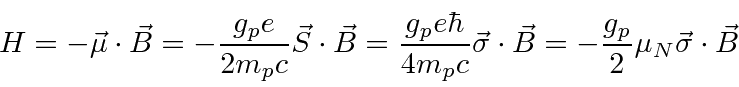
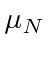 (Nuclear Magnetons).
Different nuclei will have different gyromagnetic ratios, giving us more tools to work with.
Let's choose our strong static B field to be in the z direction and the polarization on our oscillating
EM wave so that the B field points in the x direction.
The EM wave has (angular) frequency
(Nuclear Magnetons).
Different nuclei will have different gyromagnetic ratios, giving us more tools to work with.
Let's choose our strong static B field to be in the z direction and the polarization on our oscillating
EM wave so that the B field points in the x direction.
The EM wave has (angular) frequency
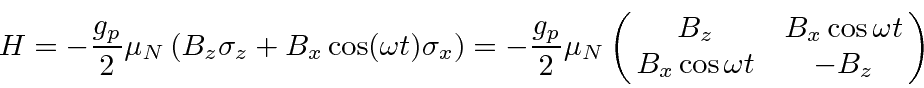
Now we apply the time dependent Schrödinger equation.
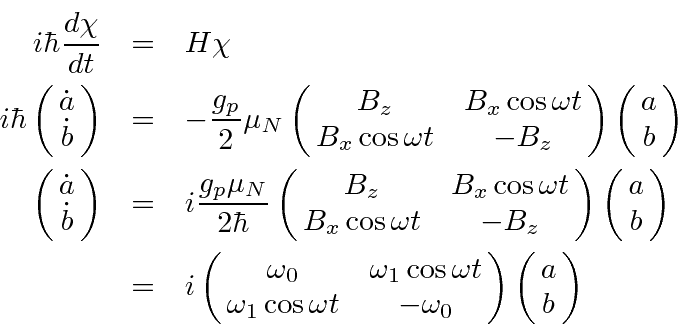
The solution
of these equations represents and early example of time
dependent perturbation theory.
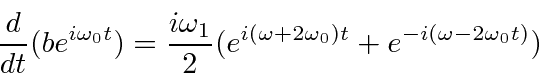
Terms that oscillate rapidly will average to zero.
The first term oscillates very rapidly.
The second term will only cause significant transitions if
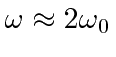 .
Note that this is exactly the condition that requires the energy of the photons in the EM field
.
Note that this is exactly the condition that requires the energy of the photons in the EM field
![]() to be equal to the energy difference between the two spin states
to be equal to the energy difference between the two spin states
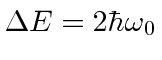 .
The conservation of energy condition must be satisfied well enough to get a significant transition rate.
Actually we will find later that for rapid transitions, energy conservation does not have to be exact.
.
The conservation of energy condition must be satisfied well enough to get a significant transition rate.
Actually we will find later that for rapid transitions, energy conservation does not have to be exact.
So we have proven that we should set the frequency
![]() of our
EM wave according to the energy difference between the two spin states. This allows us to cause
transitions to the higher energy state. In NMR, we observe the transitions back to the lower energy
state. These emit EM radiation at the same frequency and we can detect it after the stronger input
pulse ends (or by more complex methods).
We don't yet know why the higher energy state will spontaneously decay to the lower energy state.
To calculate this, we will have to quantize the field.
But we already see that the energy terms
of our
EM wave according to the energy difference between the two spin states. This allows us to cause
transitions to the higher energy state. In NMR, we observe the transitions back to the lower energy
state. These emit EM radiation at the same frequency and we can detect it after the stronger input
pulse ends (or by more complex methods).
We don't yet know why the higher energy state will spontaneously decay to the lower energy state.
To calculate this, we will have to quantize the field.
But we already see that the energy terms
![]() of standard wave mechanics will require energy conservation
with photon energies of
of standard wave mechanics will require energy conservation
with photon energies of
![]() .
.
NMR is a powerful tool in chemical analysis because the molecular field adds to the external B field so that the resonant frequency depends on the molecule as well as the nucleus. We can learn about molecular fields or just use NMR to see what molecules are present in a sample.
In MRI, we typically concentrate on one nucleus like hydrogen. We can put a gradient in
![]() so that only
a thin slice of the material has
so that only
a thin slice of the material has
![]() tuned to the resonant frequency. Therefore we can excite transitions
to the higher energy state in only a slice of the sample. If we vary (in the orthogonal direction!)
the B field during the decay of the excited state, we can get a two dimensional picture.
If we vary B as a function of time during the decay, we can get to 3D.
While there are more complex methods used in MRI, we now understand the basis of the technique.
MRIs are a very safe way to examine the inside of the body. All the field variation takes some time though.
Ultimately, a very powerful tool for scanning materials (a la Star Trek) is possible.
tuned to the resonant frequency. Therefore we can excite transitions
to the higher energy state in only a slice of the sample. If we vary (in the orthogonal direction!)
the B field during the decay of the excited state, we can get a two dimensional picture.
If we vary B as a function of time during the decay, we can get to 3D.
While there are more complex methods used in MRI, we now understand the basis of the technique.
MRIs are a very safe way to examine the inside of the body. All the field variation takes some time though.
Ultimately, a very powerful tool for scanning materials (a la Star Trek) is possible.
Jim Branson 2013-04-22