Next: Homework Problems Up: Derivations and Computations Previous: Derive Spin Rotation Matrices Contents
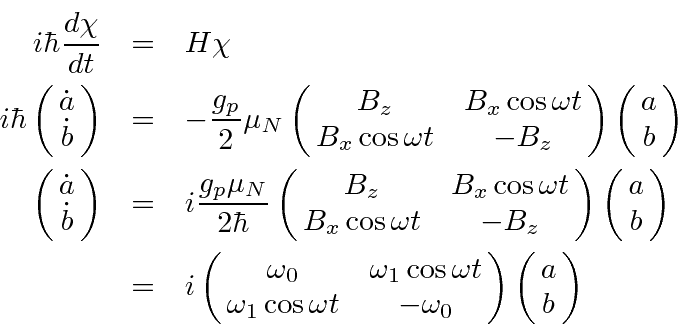
So far all we have done is plugged things into the Schrödinger equation. Now we have to solve this
system of two equations. This could be hard but we will do it only near
![]() , when the EM wave starts.
Assume that at
, when the EM wave starts.
Assume that at
![]() ,
,
![]() and
and
![]() , that is, the nucleus is in the lower energy state. Then we have
, that is, the nucleus is in the lower energy state. Then we have
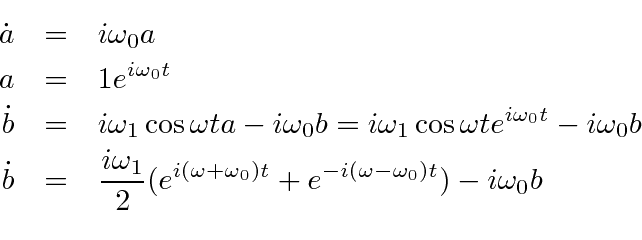
Now comes the one tricky part of the calculation.
The diagonal terms in the Hamiltonian cause a very rapid time dependence to the amplitudes.
To get b to grow, we need to keep adding
![]() in phase with b.
To see that clearly, let's compute the time derivative of
in phase with b.
To see that clearly, let's compute the time derivative of
![]() .
.
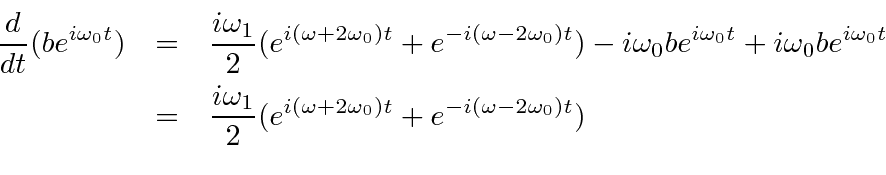
Terms that oscillate rapidly will average to zero. To get a net change in
![]() , we need to have
, we need to have
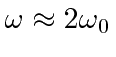 . Then the first term is important and we can neglect the second which
oscillates with a frequency of the order of
. Then the first term is important and we can neglect the second which
oscillates with a frequency of the order of
![]() .
Note that this is exactly the condition that requires the energy of the photons in the EM field
.
Note that this is exactly the condition that requires the energy of the photons in the EM field
![]() to be equal to the energy difference between the two spin states
to be equal to the energy difference between the two spin states
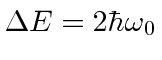 .
.
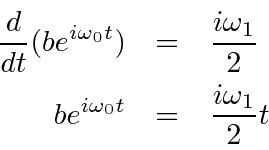
It appears that the amplitude grows linearly with time and hence the probability would grow like
![]() .
Actually, once we do the calculation (only a bit) more carefully, we will see that the probability
increases linearly with time and there is a delta function of energy conservation. We will do this
more generally in the section on time dependent perturbation theory.
.
Actually, once we do the calculation (only a bit) more carefully, we will see that the probability
increases linearly with time and there is a delta function of energy conservation. We will do this
more generally in the section on time dependent perturbation theory.
In any case, we can only cause transitions if the EM field is tuned so that
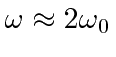 which means the photons in the EM wave have an energy equal to the difference in energy between the
spin down state and the spin up state. The transition rate increases as we increase the strength of the
oscillating B field.
which means the photons in the EM wave have an energy equal to the difference in energy between the
spin down state and the spin up state. The transition rate increases as we increase the strength of the
oscillating B field.
Jim Branson 2013-04-22