Next: Time Development of a Up: Examples Previous: Eigenvectors of for Spin Contents
As an example, lets take the
![]() direction to be in the
direction to be in the
![]() plane, between the positive
plane, between the positive
![]() and
and
![]() axes,
30 degrees from the x axis.
The unit vector is then
axes,
30 degrees from the x axis.
The unit vector is then
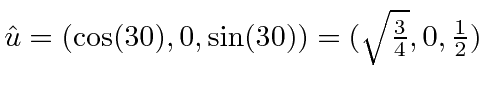 .
We may simply calculate the matrix
.
We may simply calculate the matrix
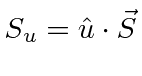 .
.
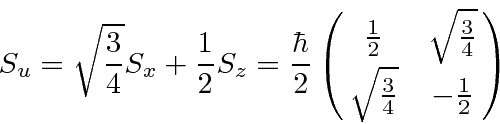
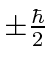 as for all axes.
as for all axes.
Factoring out the
![]() , the equation for the eigenvectors is.
, the equation for the eigenvectors is.
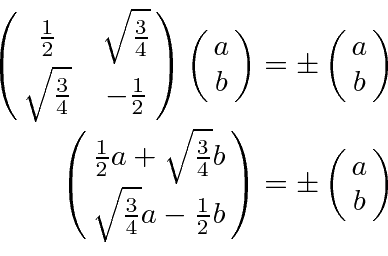
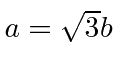 , giving the eigenvector
, giving the eigenvector
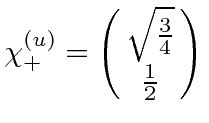 .
For the negative eigenvalue, we have
.
For the negative eigenvalue, we have
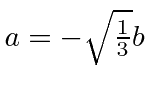 , giving the eigenvector
, giving the eigenvector
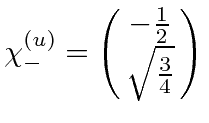 .
Of course each of these could be multiplied by an arbitrary phase factor.
.
Of course each of these could be multiplied by an arbitrary phase factor.
There is an alternate way to solve the problem using rotation matrices.
We take the states
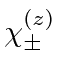 and rotate the axes so that the
and rotate the axes so that the
![]() axis is where the
axis is where the
![]() axis was.
We must think carefully about exacty what rotation to do.
Clearly we need a rotation about the
axis was.
We must think carefully about exacty what rotation to do.
Clearly we need a rotation about the
![]() axis.
Thinking about the signs carefully, we see that a rotation of -60 degrees moves the
axis.
Thinking about the signs carefully, we see that a rotation of -60 degrees moves the
![]() axis to the old
axis to the old
![]() axis.
axis.
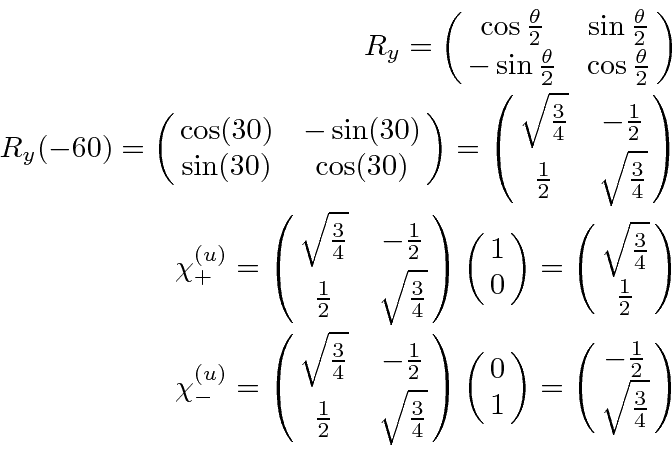
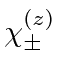 .
For most problems, this is not important but it is for some.
.
For most problems, this is not important but it is for some.
Jim Branson 2013-04-22