Next: Time Development of an Up: Examples Previous: Energy Eigenstates of an Contents
Now that we have the shorthand notation for a Stern-Gerlach apparatus,
we can put some together and think about what happens.
The following is a simple example in which three successive apparati separate the atomic beam
using a field gradient along the z direction.
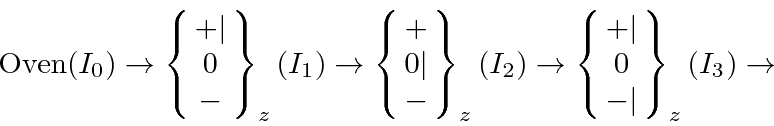
If the intensity coming out of the oven is ![]() , what are the intensities at positions 1, 2, and 3?We assume an unpolarized beam coming out of the oven so that 1/3 of the atoms will go into each initial beam in apparatus 1.
This is essentially a classical calculation since we don't know the exact state of the particles coming from the oven.
Now apparatus 1 removes the
, what are the intensities at positions 1, 2, and 3?We assume an unpolarized beam coming out of the oven so that 1/3 of the atoms will go into each initial beam in apparatus 1.
This is essentially a classical calculation since we don't know the exact state of the particles coming from the oven.
Now apparatus 1 removes the
![]() component of the beam, leaving a state with a mixture of
component of the beam, leaving a state with a mixture of
![]() and
and
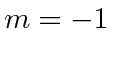 .
.
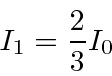
The beam will split into only two parts in the second apparatus since there is no
![]() component left.
Apparatus 2 blocks the
component left.
Apparatus 2 blocks the
![]() part, now leaving us with a state that we can write.
part, now leaving us with a state that we can write.
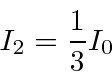
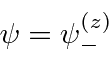
The beam in apparatus 3 all goes along the same path, the lower one.
Apparatus 3 blocks that path.
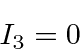
The following is a more complex example using a field gradients in the z and x directions
(assuming the beam is moving in y).
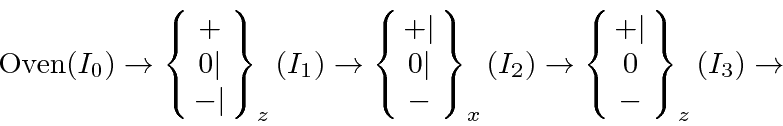
Now we have a Quantum Mechanics problem.
After the first apparatus, we have an intensity as before
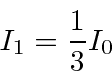
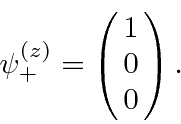
The second apparatus is oriented to separate the beam in the x direction.
The beam separates into 3 parts.
We can compute the intensity of each but lets concentrate on the bottom one because we block the other two.
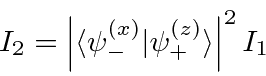
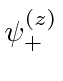 ,
goes into the state
,
goes into the state
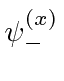 when measured in the x direction
(times the intensity coming into the apparatus).
Lets compute that probability.
when measured in the x direction
(times the intensity coming into the apparatus).
Lets compute that probability.
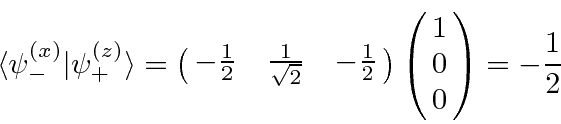
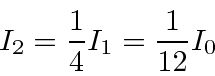
The third apparatus goes back to a separation in z and blocks the
![]() component.
The incoming state is
component.
The incoming state is
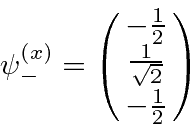
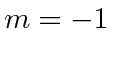 beam.
beam.

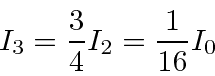
Now lets see what happens if we remove the blocking in apparatus 2.
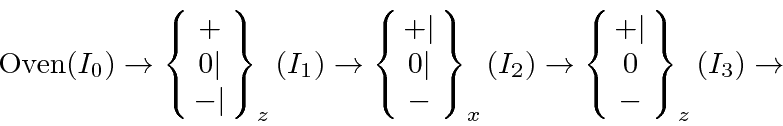
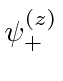 .
The intensity coming out of apparatus 2 is
.
The intensity coming out of apparatus 2 is
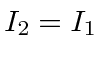 .
Now with the pure state
.
Now with the pure state
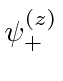 going into apparatus 3 and the top beam being blocked there,
no particles come out of apparatus 3.
going into apparatus 3 and the top beam being blocked there,
no particles come out of apparatus 3.
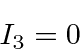
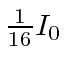 to zero.
How could this happen?
to zero.
How could this happen?
What would happen if there were bright lights in apparatus 2?
Jim Branson 2013-04-22