Next: Expectation of in General Up: Examples Previous: A series of Stern-Gerlachs Contents
We wish to determine how an angular momentum 1 state
develops with time,
develops with time,
in an applied B field.
In particular, if an atom is in the state with x component of angular momentum equal to
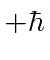 ,
,
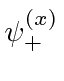 , what is the state at a later time
, what is the state at a later time
![]() ?
What is the expected value of
?
What is the expected value of
![]() as a function of time?
as a function of time?
We will choose the z axis so that the B field is in the z direction.
Then we know the energy eigenstates are the eigenstates of
![]() and are the
basis states for our vector representation of the wave function. Assume that
we start with a general state which is known at
and are the
basis states for our vector representation of the wave function. Assume that
we start with a general state which is known at
![]() .
.
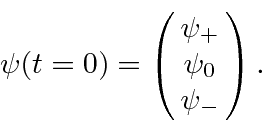
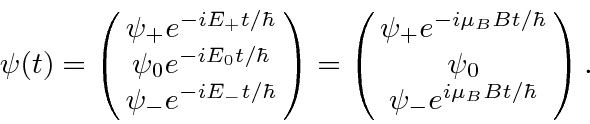
As a concrete example, let's assume we start out in the eigenstate of
![]() with eigenvalue
with eigenvalue
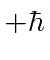 .
.
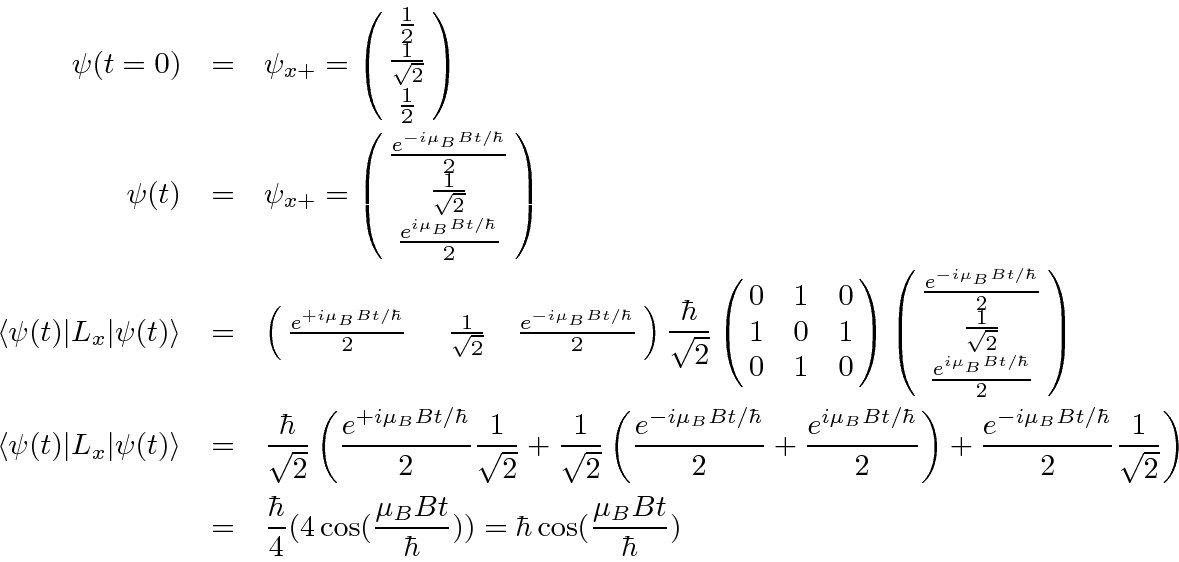
Note that this agrees with what we expect at
![]() and is consistent with the angular momentum
precessing about the z axis. If we checked
and is consistent with the angular momentum
precessing about the z axis. If we checked
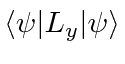 , we would see a sine instead
of a cosine, confirming the precession.
, we would see a sine instead
of a cosine, confirming the precession.
Jim Branson 2013-04-22