Next: Derivations and Computations Up: The Schrödinger Equation Previous: The Schrödinger Wave Equation Contents
Second order differential equations, like the Schrödinger Equation, can be solved by separation of variables. These separated solutions can then be used to solve the problem in general.
Assume that we can factorize the solution between time and space.
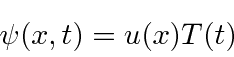
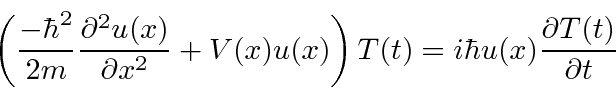
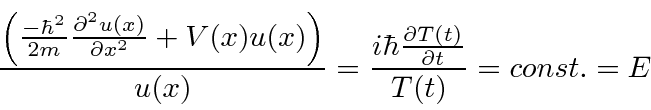
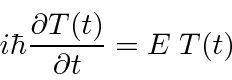
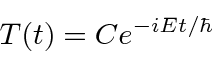
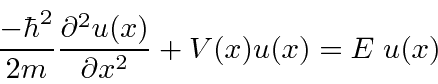
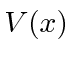 ).
).
The
![]() equation is often called the Time Independent Schrödinger Equation.
equation is often called the Time Independent Schrödinger Equation.
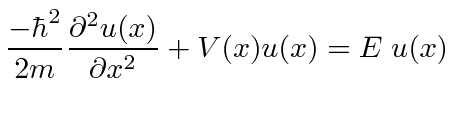 |
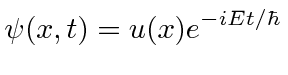 |
* Example:
Solve the Schrödinger equation for a constant potential ![]() .*
.*
Jim Branson 2013-04-22