Solution to the Schrödinger Equation in a Constant Potential

Assume we want to solve the Schrödinger Equation in a region in which the potential is constant and equal to $V_0$. We will find two solutions for each energy $E$.

We have the equation.

$$\bgroup\color{black} {-\hbar^2 \over 2m}{\partial^2\psi(x)\over\partial x^2}+V_0\psi(x)=E\psi(x) \egroup$$

$$\bgroup\color{black} {\partial^2\psi(x)\over\partial x^2}=-{2m\over\hbar^2}(E-V_0)\psi(x) \egroup$$

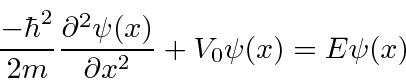
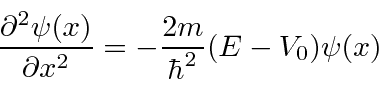
Remember that $x$ is an independent variable in the above equation while $p$ and $E$ are constants to be determined in the solution.

For 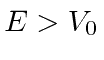$E>V_0$, there are solutions

$$\bgroup\color{black} e^{ikx} \egroup$$

and

$$\bgroup\color{black} e^{-ikx} \egroup$$

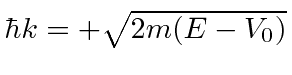if we define $k$ by the equation $\hbar k=+\sqrt{2m(E-V_0)}$. These are waves traveling in opposite directions with the same energy (and magnitude of momentum).

We could also use the linear combinations of the above two solutions

$$\bgroup\color{black} \sin(kx) \egroup$$

and

$$\bgroup\color{black} \cos(kx) .\egroup$$

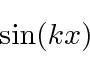
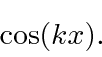
There are only two linearly independent solutions. We need to choose either the exponentials or the trig functions, not both. The sin and cos solutions represent states of definite energy but contain particles moving to the left and to the right. They are not definite momentum states. They will be useful to us for some solutions.

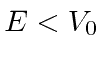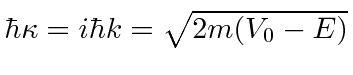The solutions are also technically correct for $E<V_0$ but $k$ becomes imaginary. Lets write the solutions in terms of $\hbar\kappa=i\hbar k=\sqrt{2m(V_0-E)}$ The solutions are

$$\bgroup\color{black} e^{\kappa x}\egroup$$

and

$$\bgroup\color{black} e^{-\kappa x} .\egroup$$

These are not waves at all, but real exponentials. Note that these are solutions for regions where the particle is not allowed classically, due to energy conservation; the total energy is less than the potential energy. We will use these solutions in Quantum Mechanics.