The Schrödinger Wave Equation

The normal equation we get, for waves on a string or on water, relates the second space derivative to the second time derivative. The Schrödinger equation uses only the first time derivative, however, the addition of the $i$ relates the real part of the wave function to the imaginary part, in effect shifting the phase by 90 degrees as the 2nd derivative would do.

$$\bgroup\color{black} {-\hbar^2 \over 2m}{\partial^2\psi(x,t)\... ...+V(x)\psi(x,t) =i\hbar{\partial\psi(x,t)\over\partial t}\egroup$$

The Schrödinger equation is built for complex wave functions.

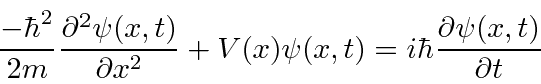
When Dirac tried to make a relativistic version of the equation, where the energy relation is a bit more complicated, he discovered new physics.

Gasiorowicz Chapter 3

Griffiths Chapter 1

Cohen-Tannoudji et al. Chapter