The Flux of Probability *

In analogy to the Poynting vector for EM radiation, we may want to know the probability currentin some physical situation. For example, in our free particle solution, the probability density is uniform over all space, but there is a net flow along the direction of the momentum.

We can derive an equation showing conservation of probability by differentiating 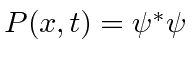$P(x,t)=\psi^*\psi$ and using the Schrödinger Equation.

$$\bgroup\color{black} {\partial P(x,t)\over\partial t}+{\partial j(x,t)\over\partial x}=0 \egroup$$

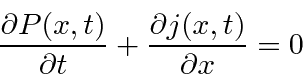
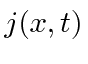This is the usual conservation equation if $j(x,t)$ is identified as the probability current.

$$\bgroup\color{black} j(x,t)={\hbar\over 2mi} \left[\psi^*{\pa... ...r\partial x}-{\partial\psi^*\over\partial x}\psi\right] \egroup$$

This current can be computed from the wave function.

If we integrate if over some interval in $x$

$$\bgroup\color{black} \int\limits_a^b{\partial P(x,t)\over\partial t}dx=-\int\limits_a^b{\partial j(x,t)\over\partial x} \egroup$$

$$\bgroup\color{black} {\partial\over\partial t}\int\limits_a^b P(x,t)dx=j(x=a,t)-j(x=b,t) \egroup$$

the equation says that the rate of change of probability in an interval is equal to the probability flux into the integral minus the flux out.

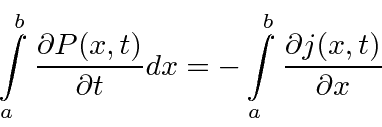
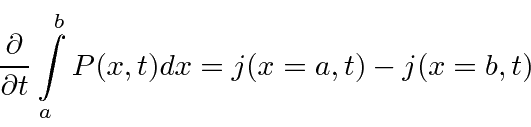
Extending this analysis to 3 dimensions,

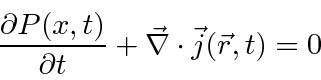
$$\bgroup\color{black} {\partial P(x,t)\over\partial t}+\vec{\nabla}\cdot \vec{j}(\vec{r},t)=0 \egroup$$

with

$$\vec{j}(\vec{r},t)={\hbar\over 2mi} \left[\ps... ...bla}\psi(\vec{r},t)-\psi(\vec{r},t)\vec{\nabla}\psi^*(\vec{r},t)\right]$$