Probability Conservation Equation *

Start from the probability and differentiate with respect to time.

$$\bgroup\color{black} {\partial P(x,t)\over\partial t}={\parti... ...rtial t}\psi-\psi^*{\partial\psi\over\partial t}\right] \egroup$$

Use the Schrödinger Equation

$$\bgroup\color{black} {-\hbar^2 \over 2m}{\partial^2\psi\over\partial x^2}+V(x)\psi=i\hbar{\partial\psi\over\partial t} \egroup$$

and its complex conjugate

$$\bgroup\color{black} {-\hbar^2 \over 2m}{\partial^2\psi^*\ove... ...x^2}+V(x)\psi^*=-i\hbar{\partial\psi^*\over\partial t} .\egroup$$

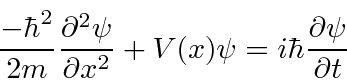
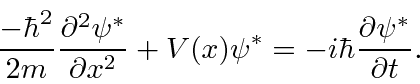
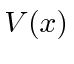(We assume $V(x)$ is real. Imaginary potentials do cause probability not to be conserved.)

Now we need to plug those equations in.

$$\bgroup\color{black} {\partial P(x,t)\over\partial t}={1\over... ...{\partial^2\psi\over\partial x^2}+V(x)\psi^*\psi\right] \egroup$$

$$\bgroup\color{black} ={1\over i\hbar}{\hbar^2 \over 2m}\left[... ...tial x}\psi-\psi^*{\partial\psi\over\partial x} \right] \egroup$$

This is the usual conservation equation if 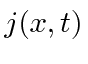$j(x,t)$ is identified as the probability current.

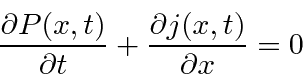
$$\bgroup\color{black} {\partial P(x,t)\over\partial t}+{\partial j(x,t)\over\partial x}=0 \egroup$$

$$\bgroup\color{black} j(x,t)={\hbar\over 2mi} \left[\psi^*{\pa... ...r\partial x}-{\partial\psi^*\over\partial x}\psi\right] \egroup$$