Next: The Angular Momentum Matrices* Up: Operators Matrices and Spin Previous: Operators Matrices and Spin Contents
We will define our vectors and matrices using a
complete set of, orthonormal basis states
![]() , usually the set of eigenfunctions of a Hermitian operator.
These basis states are analogous to the orthonormal unit vectors in Euclidean space
, usually the set of eigenfunctions of a Hermitian operator.
These basis states are analogous to the orthonormal unit vectors in Euclidean space
![]() .
.
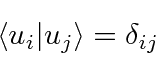
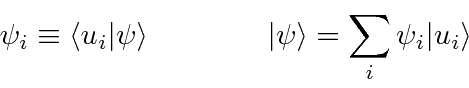
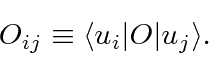
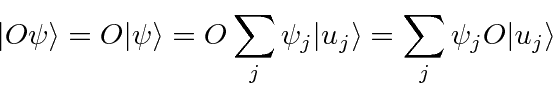
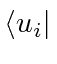 into this equation from the left, we get
into this equation from the left, we get
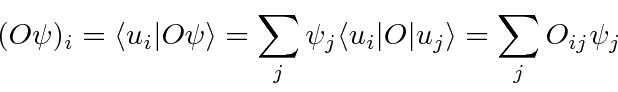

Similarly, we can look at the product of two operators
(using the identity
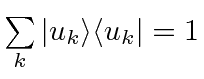 ).
).
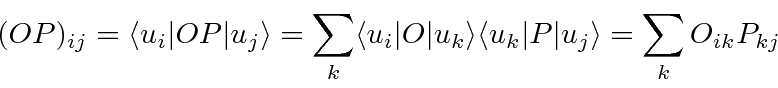
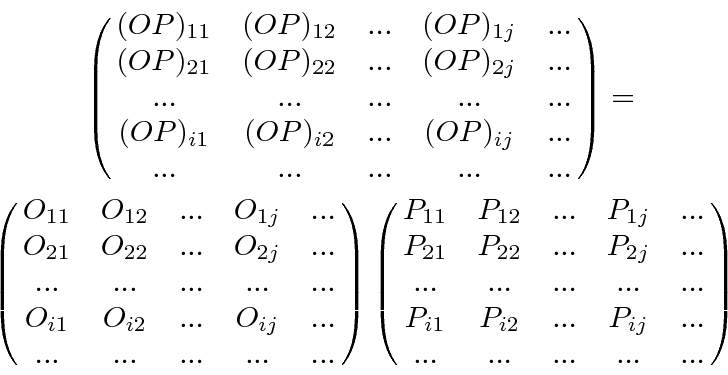
So, wave functions are represented by vectors and operators by matrices, all in the space of orthonormal functions.
* Example:
The Harmonic Oscillator Hamiltonian Matrix.*
* Example:
The harmonic oscillator raising operator.*
* Example:
The harmonic oscillator lowering operator.*
Now compute the matrix for the
Hermitian Conjugate
of an operator.
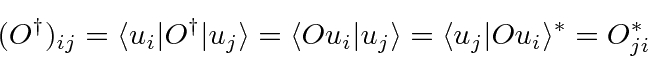
Check that this is true for ![]() and
and ![]() .
.
We know that there is a difference between a bra vector and a ket vector.
This becomes explicit in the matrix representation.
If
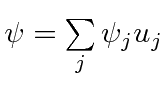 and
and
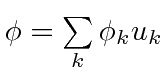 then, the dot product is
then, the dot product is
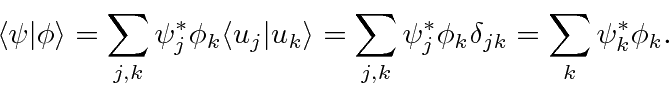
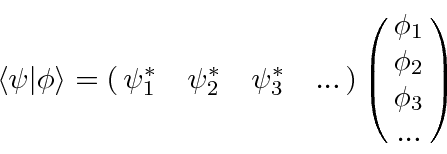
Jim Branson 2013-04-22