Next: Hermitian Conjugate of an Up: Eigenfunctions, Eigenvalues and Vector Previous: Eigenfunctions, Eigenvalues and Vector Contents
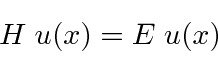
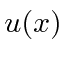 the eigenfunction,
giving a constant
the eigenfunction,
giving a constant
Usually, for bound states, there are many eigenfunction solutions (denoted here by the index
![]() ).
).
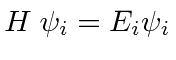 |
For states representing one particle (particularly bound states) we must
require that the solutions be normalizable.
Solutions that are not normalizable must be discarded.
A normalizable wave function must go to zero at infinity.
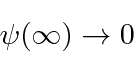
We will prove later that the eigenfunctions are orthogonal to each other.
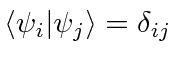 |
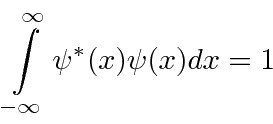
We will assume that the
eigenfunctions form a complete set
so that any function can be written as a linear combination of them.
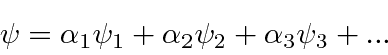
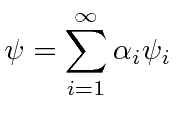 |
Since the eigenfunctions are orthogonal, we can easily
compute the coefficients
in the expansion of an arbitrary wave function
![]() .
.
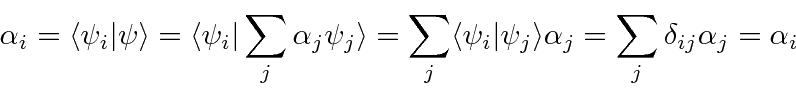
We will later think of the eigenfunctions as unit
vectors in a vector space.
The arbitrary wave function
![]() is then a vector in that space.
is then a vector in that space.
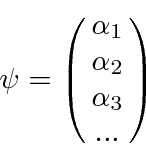
It is instructive to compute the expectation value of the Hamiltonianusing the expansion of
![]() and the orthonormality of the eigenfunctions.
and the orthonormality of the eigenfunctions.
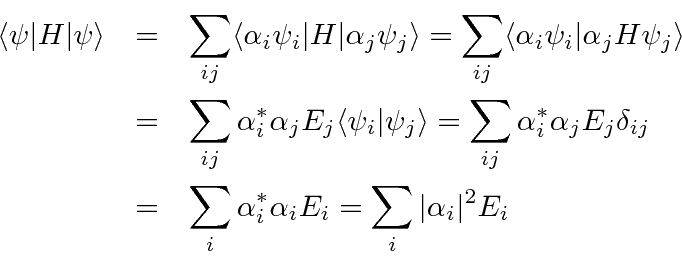
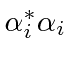 obviously give the probability.
obviously give the probability.
Jim Branson 2013-04-22