Next: Continuity of Wavefunctions and Up: Derivations and Computations Previous: Derivations and Computations Contents
We wish to prove that eigenfunctions of Hermitian operators are orthogonal. In fact we will first do this except in the case of equal eigenvalues.
Assume we have a Hermitian operator ![]() and two of its eigenfunctions such that
and two of its eigenfunctions such that
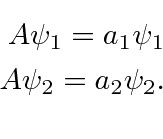
Now we compute
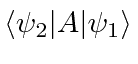 two ways.
two ways.
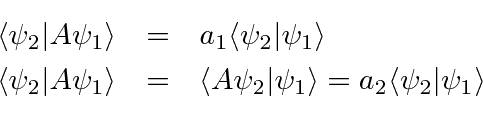
Now we subtract the two equations.
The left hand sides are the same so they give zero.
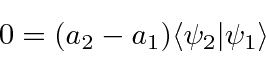
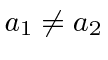 then
then
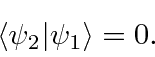
What if two of the eigenfunctions have the same eigenvalue?
Then, our proof doesn't work.
Assume
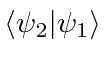 is real, since we can always adjust a
phase to make it so.
Since any linear combination of
is real, since we can always adjust a
phase to make it so.
Since any linear combination of
![]() and
and
![]() has the same eigenvalue,
we can use any linear combination.
Our aim will be to choose two linear combinations which are orthogonal.
Lets try
has the same eigenvalue,
we can use any linear combination.
Our aim will be to choose two linear combinations which are orthogonal.
Lets try
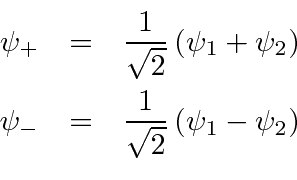
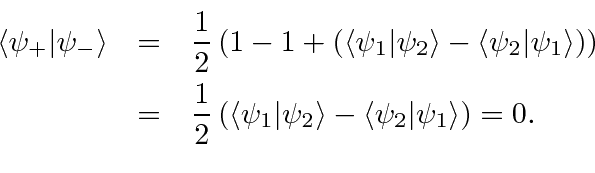
We have thus found an orthogonal set of eigenfunctions even in the case that some of the eigenvalues are equal (degenerate). From now on we will just assume that we are working with an orthogonal set of eigenfunctions.
Jim Branson 2013-04-22