Next: The Particle in a Up: Eigenfunctions, Eigenvalues and Vector Previous: Hermitian Operators Contents
Wavefunctions are analogous to vectors in 3D space. The unit vectors of our vector space are eigenstates.
In normal 3D space, we represent a vector by its components.
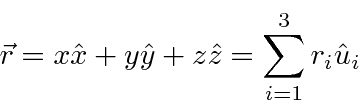
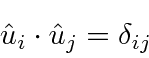
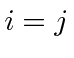 and otherwise equal to zero.
and otherwise equal to zero.
Eigenfunctions - the unit vectors of our space - are orthonormal.
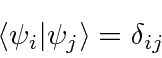
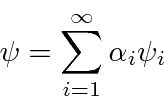
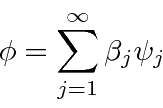
In normal 3D space, we can compute the
dot product between two vectors using the components.
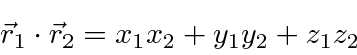
In our vector space, we define the dot product to be
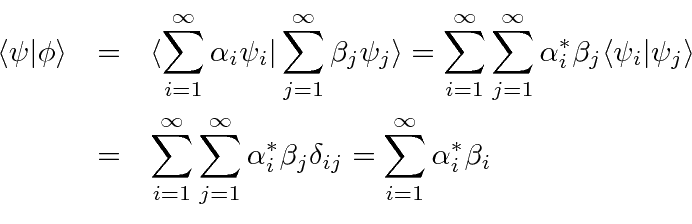
From a more mathematical point of view, the square integrable functions form a (vector) Hilbert Space.
The scalar product is defined as above.
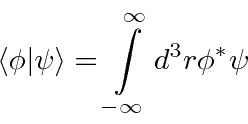
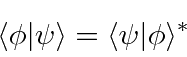
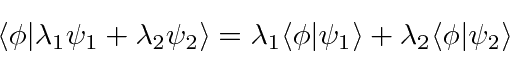
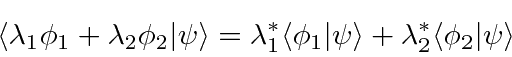
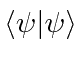 is real and greater than 0.
It equals zero iff
is real and greater than 0.
It equals zero iff
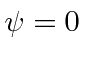 .
We may also derive the Schwartz inequality.
.
We may also derive the Schwartz inequality.
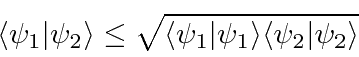
Linear operators take vectors in the space into other vectors.
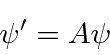
Jim Branson 2013-04-22