Next: Hermitian Operators Up: Eigenfunctions, Eigenvalues and Vector Previous: Eigenvalue Equations Contents
First let us define the Hermitian Conjugate of an operator
![]() to be
to be
![]() .
The meaning of this conjugate is given in the following equation.
.
The meaning of this conjugate is given in the following equation.
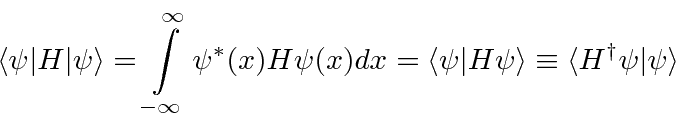
The definition of the Hermitian Conjugate of an operator can be simply written in Bra-Ket notation.
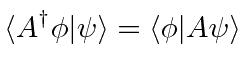 |
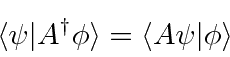
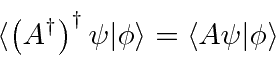
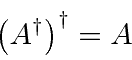
Its easy to show that
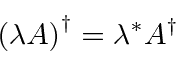
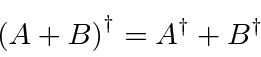
We can also show that
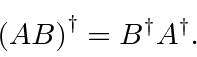
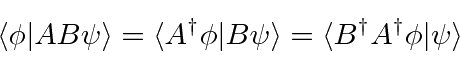
* Example:
Find the Hermitian conjugate of the operator 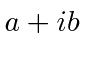 .*
.*
* Example:
Find the Hermitian conjugate of the operator
![]() .*
.*
Jim Branson 2013-04-22