Next: Eigenvalue Problems with Matrices Up: Operators Matrices and Spin Previous: The Matrix Representation of Contents
An important case of the use of the matrix form of operators is that of
Angular Momentum
Assume we have an atomic state with
![]() (fixed) but
(fixed) but
![]() free.
We may use the eigenstates of
free.
We may use the eigenstates of
![]() as a basis for our states and operators.
Ignoring the (fixed) radial part of the wavefunction,
our state vectors for
as a basis for our states and operators.
Ignoring the (fixed) radial part of the wavefunction,
our state vectors for
![]() must be a linear combination of the
must be a linear combination of the
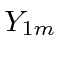
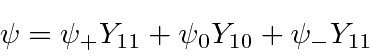
We will write our 3 component vectors like
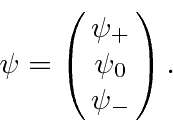
The matrices must satisfy the same commutation relations as the differential operators.
![\begin{displaymath}\bgroup\color{black} [L_x,L_y]=i\hbar L_z \egroup\end{displaymath}](img1678.png)
Since these matrices represent physical variables, we expect them to be Hermitian. That is, they are equal to their conjugate transpose. Note that they are also traceless.
As an example of the use of these matrices,
let's compute an expectation value of
![]() in the matrix representation for the general state
in the matrix representation for the general state
![]() .
.
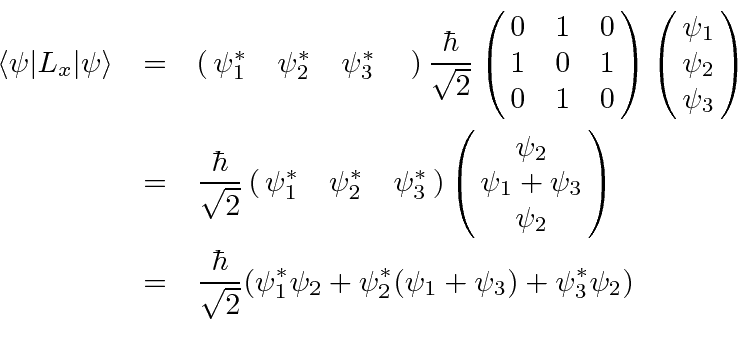
Jim Branson 2013-04-22