Next: Angular Momentum Algebra: Raising Up: Angular Momentum Previous: Angular Momentum Contents
If the potential only depends on the distance between two particles,
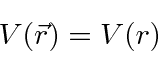
If a the Hamiltonian has rotational symmetry, we can
show that the Angular Momentum operators commute with the Hamiltonian.
![\begin{displaymath}\bgroup\color{black} [H,L_i]=0 \egroup\end{displaymath}](img1676.png)
We will not be able to label our states with the quantum numbers for the three components of angular momentum.
Recall that we are looking for a set of mutually commuting operators
to label our energy eigenstates.
We actually want two operators plus
![]() to give us three quantum numbers for states in
three dimensions.
to give us three quantum numbers for states in
three dimensions.
The
components of angular momentum do not commute
with each other
![\begin{displaymath}\bgroup\color{black} [L_x,L_y]=i\hbar L_z \egroup\end{displaymath}](img1678.png)
![\bgroup\color{black}$\displaystyle [L_i,L_j]=i\hbar\epsilon_{ijk}L_k $\egroup](img1679.png) |
![\bgroup\color{black}$\displaystyle [L^2,L_i]=0 $\egroup](img1680.png) |
These commutators lead us to choose the mutually commuting set of operators to be
![]() ,
,
![]() , and
, and
![]() .
We could have chosen any component, however, it is most convenient to choose
.
We could have chosen any component, however, it is most convenient to choose
![]() given
the standard definition of spherical coordinates.
given
the standard definition of spherical coordinates.
The
Schrödinger equation now can be rewritten
with only radial derivatives and
![]() .
.
![\begin{eqnarray*}
{-\hbar^2\over 2\mu}\nabla^2 u_E(\vec{r})+V(r)u_E(\vec{r})&=&...
...2 r^2}\right] u_E(\vec{r})+V(r)u_E(\vec{r})&=&Eu_E(\vec{r}) \\
\end{eqnarray*}](img1681.png)
It is possible to separate the Schrödinger equation since
![]() and
and
![]() appear separately.
Write the solution as a product
appear separately.
Write the solution as a product
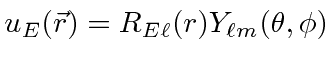 |
We get the three equations.
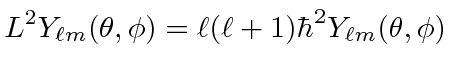
|
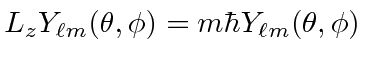
|
![\bgroup\color{black}$\displaystyle {-\hbar^2\over 2\mu}\left[{1\over r^2}\left(r...
...ell(\ell+1)\over r^2}\right]R_{E\ell}(r)+V(r)R_{E\ell}(r)=ER_{E\ell}(r) $\egroup](img1685.png) |
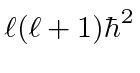 ,
we have anticipated the solution but not constrained it, since the units of
angular momentum are those of
,
we have anticipated the solution but not constrained it, since the units of
angular momentum are those of
We will use the algebra of the angular momentum operators to help us solve the angular part of the problem in general.
For any given problem with rotational symmetry, we will need to
solve a particular differential equation in one variable ![]() .
This radial equation can be simplified a bit.
.
This radial equation can be simplified a bit.
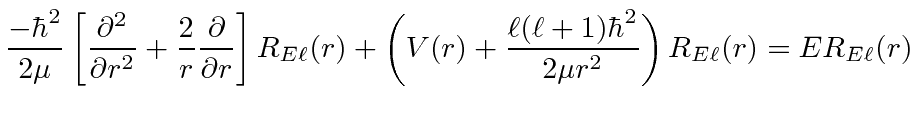 |
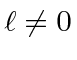 , it is like a repulsive potential.
, it is like a repulsive potential.
Jim Branson 2013-04-22