Next: The Angular Momentum Eigenfunctions Up: Angular Momentum Previous: Rotational Symmetry Contents
We have already derived the commutators of the angular momentum operators
![\begin{eqnarray*}[L_x,L_y]&=&i\hbar L_z \\
{[L_i,L_j]}&=&i\hbar\epsilon_{ijk}L_k \\
{[L^2,L_i]}&=&0 .\\
\end{eqnarray*}](img1690.png)
We have shown that angular momentum is quantized for a rotor with a single angular variable.
To progress toward the possible quantization of angular momentum variables in 3D,
we define the operator
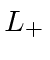 and its Hermitian conjugate
and its Hermitian conjugate
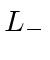 .
.
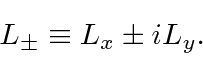
![\begin{displaymath}\bgroup\color{black} [L^2,L_\pm]=0 \egroup\end{displaymath}](img1694.png)
The commutator with
![]() is.
is.
![\begin{displaymath}\bgroup\color{black} [L_\pm,L_z]=[L_x,L_z]\pm i[L_y,L_z]=i\hbar(-L_y\pm iL_x)=\mp\hbar L_\pm .\egroup\end{displaymath}](img1695.png)
From the commutators
![\bgroup\color{black}$[L^2,L_\pm]=0$\egroup](img1696.png) and
and
![\bgroup\color{black}$[L_\pm,L_z]=\mp\hbar L_\pm$\egroup](img1697.png) ,
we can
derive the effect of the operators
,
we can
derive the effect of the operators
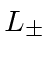 on the eigenstates
on the eigenstates
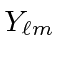 ,
and in so doing, show that
,
and in so doing, show that
![]() is an integer greater than or equal to 0,
and that
is an integer greater than or equal to 0,
and that
![]() is also an integer
is also an integer
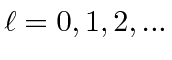
|
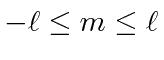
|
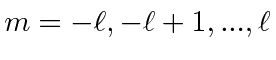
|
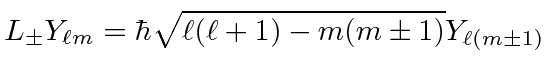 |
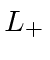 raises the
raises the
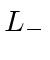 lowers it by one unit.
The raising stops when
lowers it by one unit.
The raising stops when
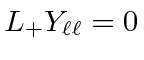 .
Similarly, the lowering stops because
.
Similarly, the lowering stops because
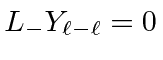 .
.

Angular momentum is quantized.
Any measurement of a component of angular momentum will give some integer times
![]() .
Any measurement of the total angular momentum gives the somewhat curious result
.
Any measurement of the total angular momentum gives the somewhat curious result
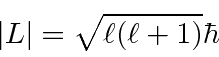
Note that we can easily write the components of angular momentum in terms of the raising and lowering operators.
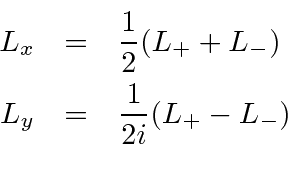
We will also find the following equations useful (and easy to compute).
![\begin{eqnarray*}[L_+,L_-]&=&i[L_y,L_x]-i[L_x,L_y]=\hbar(L_z+L_z)=2\hbar L_z \\
L^2&=&L_+L_-+L_z^2-\hbar L_z .\\
\end{eqnarray*}](img1710.png)
* Example:
What is the expectation value of ![]() in the state
in the state
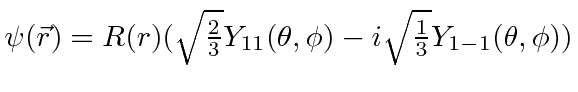 ?*
?*
* Example:
What is the expectation value of ![]() in the state
in the state
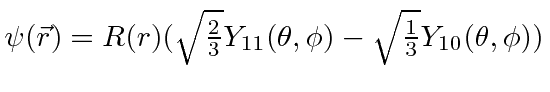 ?*
?*
Jim Branson 2013-04-22