Rotational Symmetry Implies Angular Momentum Conservation

In three dimensions, this means that we can change our coordinates by rotating about any one of the axes and the equations should not change. Lets try and infinitesimal rotation about the $z$ axis. The $x$ and $y$ coordinates will change.

$$\begin{eqnarray*} x'=x+d\theta y \\ y'=y-d\theta x \\ \end{eqnarray*}$$

The original Schrödinger Equation is

$$\bgroup\color{black} H\psi(x,y,z)=E\psi(x,y,z) \egroup$$

and the transformed equation is

$$\bgroup\color{black} H\psi(x+d\theta y,y-d\theta x,z)=E\psi(x+d\theta y,y-d\theta x,z) .\egroup$$

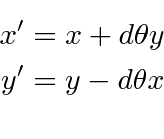
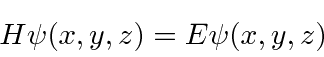
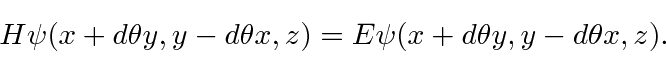
Now we Taylor expand this equation.

$$\bgroup\color{black} H\psi(x,y,z)+Hd\theta\left({\partial\psi... ...ver\partial x}y -{\partial\psi\over\partial y}x\right) \egroup$$

Subtract off the original equation.

$$\bgroup\color{black} H\left({\partial\over\partial x}y-{\part... ...over\partial x}y-{\partial\over\partial y}x\right)H\psi \egroup$$

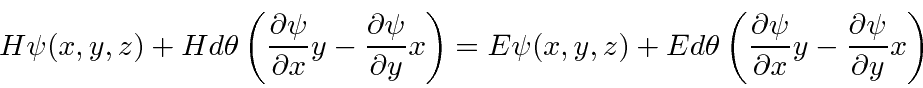
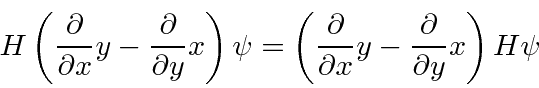
We find an operator that commutes with the Hamiltonian.

$$\bgroup\color{black} \left[H,{\hbar\over i}\left(x{\partial\over\partial y}-y{\partial\over\partial x}\right)\right]=0 \egroup$$

Note that we have inserted the constant ${\hbar\over i}$ in anticipation of identifying this operator as the $z$ component of angular momentum.

$$\bgroup\color{black} \vec{L}=\vec{r}\times\vec{p} \egroup$$

$$\bgroup\color{black} L_z={\hbar\over i}\left(x{\partial\over\partial y}-y{\partial\over\partial x}\right) =xp_y-yp_x \egroup$$

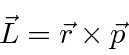
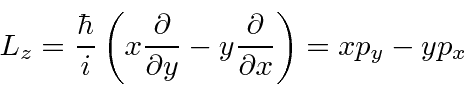
We could have done infinitesimal rotations about the $x$ or $y$ axes and shown that all the components of the angular momentum operator commute with the Hamiltonian.

$$\bgroup\color{black}[H,L_z]=[H,L_x]=[H,L_y]=0\egroup$$

Remember that operators that commute with the Hamiltonian imply physical quantities that are conserved.