The Commutators of the Angular Momentum Operators
however, the square of the angular momentum vector commutes with all the components.
This will give us the operators we need to label states in 3D central potentials.
Lets just compute the commutator.
Since there is no difference between
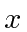 ,
,
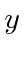 and
and
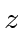 ,
we can generalize this to
,
we can generalize this to
where
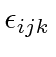 is the completely antisymmetric tensor
and we assume a sum over repeated indices.
is the completely antisymmetric tensor
and we assume a sum over repeated indices.
The tensor is equal to 1 for cyclic permutations of 123,
equal to -1 for anti-cyclic permutations,
and equal to zero if any index is repeated.
It is commonly used for a cross product.
For example, if
then
where we again assume a sum over repeated indices.
Now lets compute commutators of the
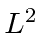 operator.
operator.
We can generalize this to
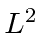 commutes with every component of
commutes with every component of
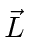 .
.
Jim Branson
2013-04-22
![\begin{displaymath}\bgroup\color{black} [L_x,L_y]\neq 0 ,\egroup\end{displaymath}](img1749.png)
![\begin{displaymath}\bgroup\color{black}[L^2,L_z]=0\egroup\end{displaymath}](img237.png)
![\begin{eqnarray*}[L_x,L_y]&=&[yp_z-zp_y,zp_x-xp_z]=y[p_z,z]p_x+[z,p_z]p_yx \\
&=&{\hbar\over i}[yp_x-xp_y]=i\hbar L_z \\
\end{eqnarray*}](img1750.png)
![\begin{displaymath}\bgroup\color{black} [L_i,L_j]=i\hbar\epsilon_{ijk}L_k \egroup\end{displaymath}](img1751.png)
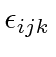 is the completely antisymmetric tensor
and we assume a sum over repeated indices.
is the completely antisymmetric tensor
and we assume a sum over repeated indices.
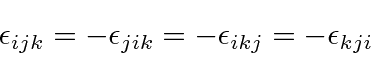
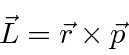
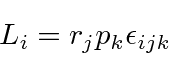
![]() operator.
operator.
![\begin{eqnarray*}
L^2&=&L_x^2+L_y^2+L_z^2 \\
{[L_z,L^2]}&=&[L_z,L_x^2]+[L_z,L...
..._y[L_z,L_y] \\
&=&i\hbar (L_yL_x+L_xL_y-L_xL_y-L_yL_x)=0 \\
\end{eqnarray*}](img1755.png)
![\begin{displaymath}\bgroup\color{black} [L_i,L^2]=0 .\egroup\end{displaymath}](img1756.png)