Next: Operators Matrices and Spin Up: Quantum Physics 130 Previous: Sample Test Problems Contents
We have already solved the problem of a 3D harmonic oscillator by
separation of variables in Cartesian coordinates.
It is instructive to
solve the same problem in spherical coordinatesand compare the results.
The potential is
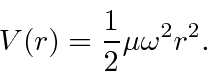
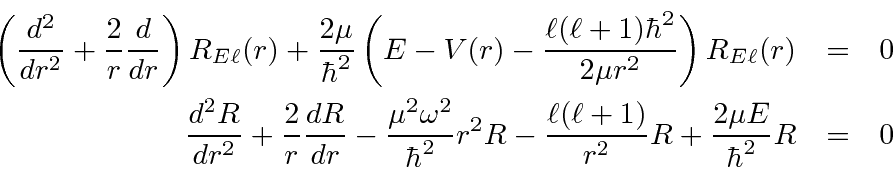
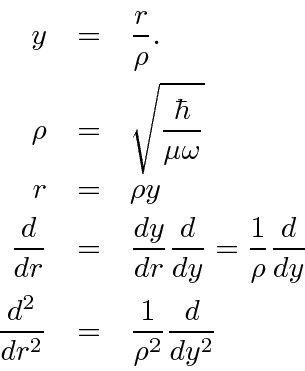
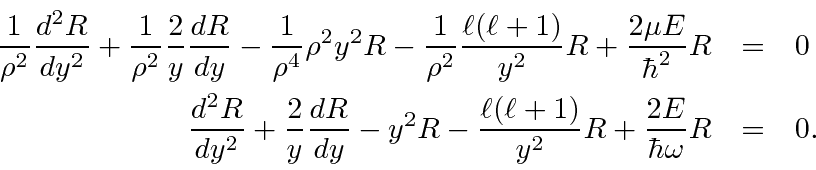
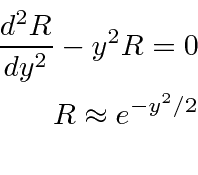
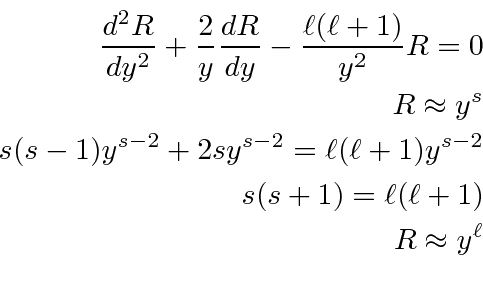
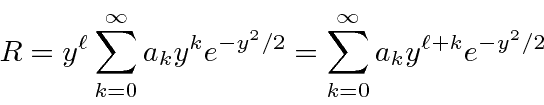
We'll need to compute the derivatives.
![\begin{eqnarray*}
{dR\over dy}=\sum\limits_{k=0}^\infty a_k
[(\ell+k)y^{\ell+k-1...
...ell+k-2} \\
-(2\ell+2k+1)y^{\ell+k}+y^{\ell+k+2}]e^{-y^2/2} \\
\end{eqnarray*}](img2082.png)
We can now plug these into the radial equation.
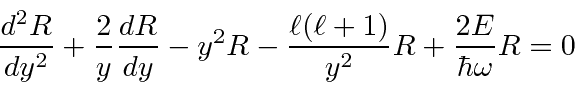
![\begin{eqnarray*}
\sum\limits_{k=0}^\infty a_k \left[
(\ell+k)(\ell+k-1)y^{\ell+...
...ell+1)y^{\ell+k-2}
+{2E\over\hbar\omega}y^{\ell+k}
\right]=0 \\
\end{eqnarray*}](img2085.png)
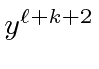 and some of the terms for small
and some of the terms for small
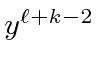 should cancel
if we did our job right.
should cancel
if we did our job right.
![\begin{eqnarray*}
\sum\limits_{k=0}^\infty a_k \left[
[(\ell+k)(\ell+k-1)-\ell(\...
...{2E\over\hbar\omega}-(2\ell+2k+3)\right]y^{\ell+k}
\right]=0 \\
\end{eqnarray*}](img2088.png)
Now as usual, the coefficient for each power of
![]() must be zero
for this sum to be zero for all
must be zero
for this sum to be zero for all
![]() .
Before shifting terms, we must examine the first few terms of this
sum to learn about conditions on
.
Before shifting terms, we must examine the first few terms of this
sum to learn about conditions on
![]() and
and
![]() .
The first term in the sum runs the risk of giving us a power of
.
The first term in the sum runs the risk of giving us a power of
![]() which cannot be canceled by the second term if
which cannot be canceled by the second term if
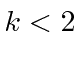 .
For
.
For
![]() , there is no problem because the term is zero.
For
, there is no problem because the term is zero.
For
![]() the term is
the term is
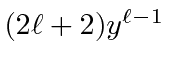 which cannot be made
zero unless
which cannot be made
zero unless
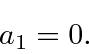
Now we will do the usual shift of the first term of the sum so
that everything has a
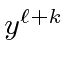 in it.
in it.
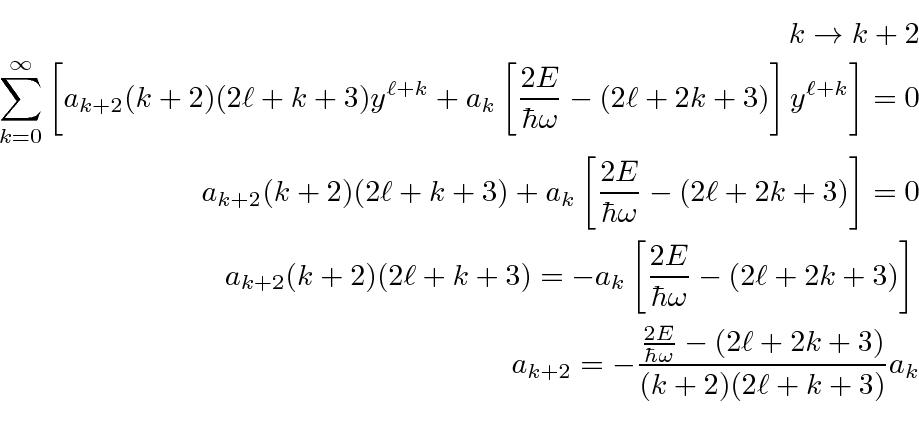
For large
![]() ,
,
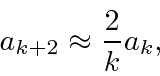
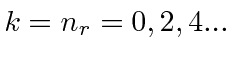 , by requiring
, by requiring
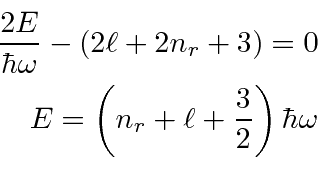
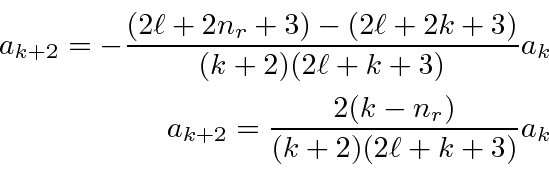
To rewrite the series in terms of
![]() and let
and let
![]() take on every integer value, we make the substitutions
take on every integer value, we make the substitutions
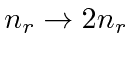 and
and
![]() in the recursion relation for
in the recursion relation for
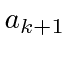 in terms of
in terms of
![]() .
.
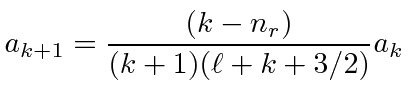
|
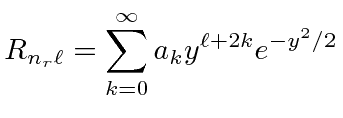
|
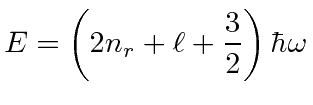 |
The table shows the quantum numbers for the states of each energy for our separation in spherical
coordinates, and for separation in Cartesian coordinates.
Remember that there are
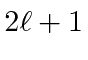 states with different
states with different
![]() components of angular momentum for the
spherical coordinate states.
components of angular momentum for the
spherical coordinate states.
|
|
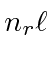 |
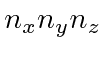 |
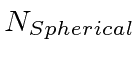 |
 |
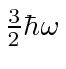 |
00 | 000 | 1 | 1 |
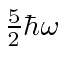 |
01 | 001(3 perm) | 3 | 3 |
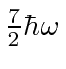 |
10, 02 | 002(3 perm), 011(3 perm) | 6 | 6 |
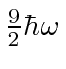 |
11, 03 | 003(3 perm), 210(6 perm), 111 | 10 | 10 |
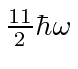 |
20, 12, 04 | 004(3), 310(6), 220(3), 211(3) | 15 | 15 |
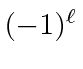 for the angular momentum states
and that it is
for the angular momentum states
and that it is
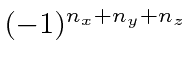 for the Cartesian states.
If we were more industrious, we could verify that the wavefunctions in spherical coordinates are just
linear combinations of the solutions in Cartesian coordinates.
for the Cartesian states.
If we were more industrious, we could verify that the wavefunctions in spherical coordinates are just
linear combinations of the solutions in Cartesian coordinates.
Jim Branson 2013-04-22