Next: Sample Test Problems Up: 3D Problems Separable in Previous: Degeneracy Pressure in Stars Contents
The 3D harmonic oscillator can also be separated in Cartesian coordinates.
For the case of a central potential,
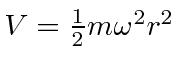 , this
problem can also be solved nicely in spherical coordinates using rotational
symmetry. The cartesian solution is easier and better for counting states though.
, this
problem can also be solved nicely in spherical coordinates using rotational
symmetry. The cartesian solution is easier and better for counting states though.
Lets assume the central potential so we can compare to our later solution. We could have three different spring constants and the solution would be as simple. The Hamiltonian is
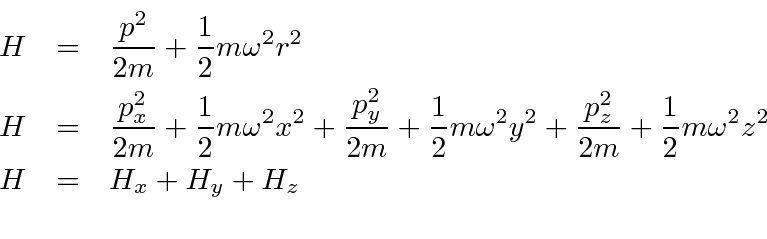
The problem separates nicely, giving us three independent harmonic oscillators.
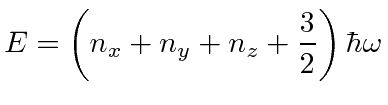
|
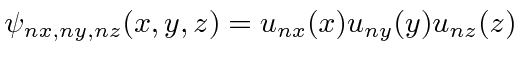 |
This was really easy.
This problem has a different Fermi surface in
![]() -space than did the particle in a box.
The boundary between filled and unfilled energy levels is a plane defined by
-space than did the particle in a box.
The boundary between filled and unfilled energy levels is a plane defined by
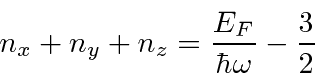
Jim Branson 2013-04-22