- A particle of mass
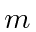 in 3 dimensions is in a potential
in 3 dimensions is in a potential
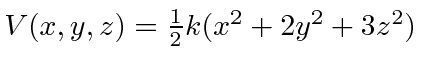 .
Find the energy eigenstates in terms of 3 quantum numbers.
What is the energy of the ground state and first excited state?
.
Find the energy eigenstates in terms of 3 quantum numbers.
What is the energy of the ground state and first excited state?
- *
N identical fermions are bound (at low temperature)
in a potential
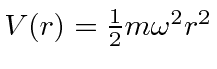 .
Use separation in Cartesian coordinates to find the energy eigenvalues in
terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
Find the Fermi energy of the system. If you are having trouble finding
the number of states with energy less than
.
Use separation in Cartesian coordinates to find the energy eigenvalues in
terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
Find the Fermi energy of the system. If you are having trouble finding
the number of states with energy less than 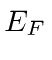 , you may assume that it
is
, you may assume that it
is
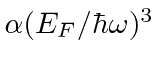 .
.
- A particle of mass m is in the potential
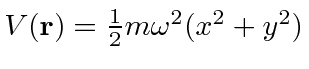 .
Find operators that commute with the Hamiltonian and use them to
simplify the Schrödinger equation. Solve this problem
in the simplest way possible to
find the eigen-energies
in terms of a set of "quantum numbers" that describe the system.
.
Find operators that commute with the Hamiltonian and use them to
simplify the Schrödinger equation. Solve this problem
in the simplest way possible to
find the eigen-energies
in terms of a set of "quantum numbers" that describe the system.
- A particle is in a cubic box. That is, the potential is
zero inside a cube of side L and infinite outside the cube. Find the
3 lowest allowed energies. Find the number of states (level of degeneracy)
at each of these 3 energies.
- A particle of mass m is bound in the 3 dimensional potential
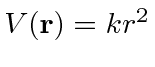 .
.
- a)
- Find the energy levels for this particle.
- b)
- Determine the number of degenerate states for the first
three energy levels.
- A particle of mass
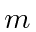 is in a cubic box. That is, the potential is
zero inside a cube of side
is in a cubic box. That is, the potential is
zero inside a cube of side 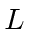 and infinite outside.
and infinite outside.
- a)
- Find the three lowest allowed energies.
- b)
- Find the number of states (level of degeneracy) at each of
these three energies.
- c)
- Find the Fermi Energy
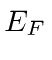 for
for 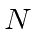 particles in the box.
(N is large.)
particles in the box.
(N is large.)
- A particle is confined in a rectangular box of length
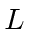 , width
, width 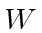 , and ``tallness''
, and ``tallness'' 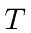 .
Find the energy eigenvalues in terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
What are the energies of the three lowest energy states if
.
Find the energy eigenvalues in terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
What are the energies of the three lowest energy states if 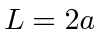 ,
, 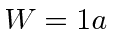 , and
, and 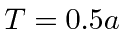 .
.
- A particle of mass m is bound in the 3 dimensional potential
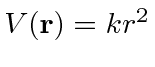 .
.
- a) Find the energy levels for this particle.
- b) Determine the number of degenerate states for the first
three energy levels.
- In 3 dimensions, a particle of mass
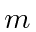 is bound in a potential
is bound in a potential
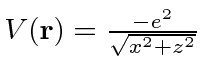 .
.
- a)
- The definite energy states will, of course,
be eigenfunctions of
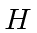 .
What other operators can they be eigenfunctions of?
.
What other operators can they be eigenfunctions of?
- b)
- Simplify the three dimensional Schr
 dinger
equation by using these operators.
dinger
equation by using these operators.
Jim Branson
2013-04-22
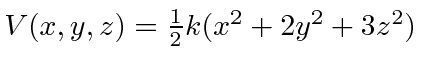 .
Find the energy eigenstates in terms of 3 quantum numbers.
What is the energy of the ground state and first excited state?
.
Find the energy eigenstates in terms of 3 quantum numbers.
What is the energy of the ground state and first excited state?
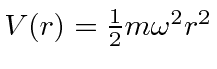 .
Use separation in Cartesian coordinates to find the energy eigenvalues in
terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
Find the Fermi energy of the system. If you are having trouble finding
the number of states with energy less than
.
Use separation in Cartesian coordinates to find the energy eigenvalues in
terms of a set of three quantum numbers (which correspond to 3
mutually commuting operators).
Find the Fermi energy of the system. If you are having trouble finding
the number of states with energy less than 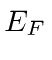 , you may assume that it
is
, you may assume that it
is
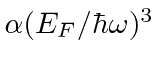 .
.
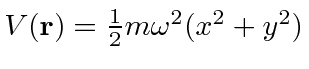 .
Find operators that commute with the Hamiltonian and use them to
simplify the Schrödinger equation. Solve this problem
in the simplest way possible to
find the eigen-energies
in terms of a set of "quantum numbers" that describe the system.
.
Find operators that commute with the Hamiltonian and use them to
simplify the Schrödinger equation. Solve this problem
in the simplest way possible to
find the eigen-energies
in terms of a set of "quantum numbers" that describe the system.
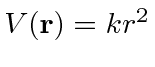 .
.
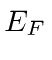 for
for 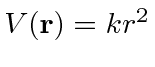 .
.
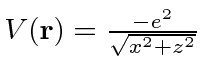 .
.