3D Problems Separable in Cartesian Coordinates

We will now look at the case of potentials that separate in Cartesian coordinates. These will be of the form.

$$\bgroup\color{black} V(\vec{r})=V_1(x)+V_2(y)+V_3(z) \egroup$$

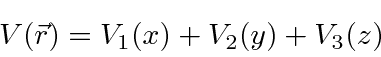
In this case, we can solve the problem by separation of variables.

$$\begin{eqnarray*} H\!\!\! &=&\!\!\! H_x+H_y+H_z \\ (H_x+H_y+H_z)u(x)v(y)w(z)\!\... ...-{(H_y+H_z)v(y)w(z)\over v(y)w(z)}\!\!\! &=&\!\!\!\epsilon_x \\ \end{eqnarray*}$$

The left hand side of this equation depends only on $x$, while the right side depends on $y$ and $z$. In order for the two sides to be equal everywhere, they must both be equal to a constant which we call $\epsilon_x$.

The $x$ part of the solution satisfies the equation

$$\bgroup\color{black} H_xu(x)=\epsilon_xu(x) .\egroup$$

Treating the other components similarly we get

$$\begin{eqnarray*} H_yv(y)=\epsilon_yv(y) \\ H_zw(z)=\epsilon_zw(z) \\ \end{eqnarray*}$$

and the total energy is

$$\bgroup\color{black} E=\epsilon_x+\epsilon_y+\epsilon_z .\egroup$$

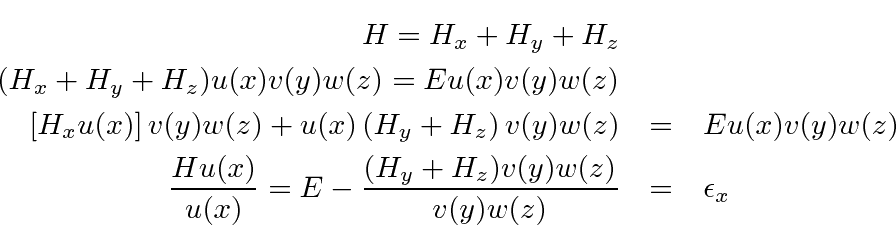
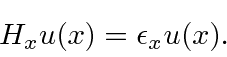
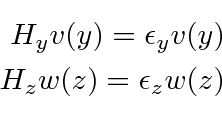
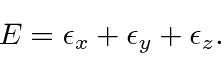
There are only a few problems which can be worked this way but they are important.