Next: Degeneracy Pressure in Stars Up: Particle in a 3D Previous: Particle in a 3D Contents
If we fill a cold box with
![]() fermions, they will all go into different low-energy states.
In fact, if the temperature is low enough, they will go into the lowest energy
fermions, they will all go into different low-energy states.
In fact, if the temperature is low enough, they will go into the lowest energy
![]() states.
states.
If we fill up all the states up to some energy, that energy is called the Fermi energy.
All the states with energies lower than
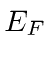 are filled, and all the states with energies
larger than
are filled, and all the states with energies
larger than
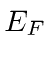 are empty.
(Non zero temperature will put some particles in excited states, but, the idea of the
Fermi energy is still valid.)
are empty.
(Non zero temperature will put some particles in excited states, but, the idea of the
Fermi energy is still valid.)
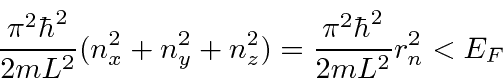
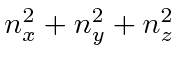 ,
it makes sense to define a radius
,
it makes sense to define a radius
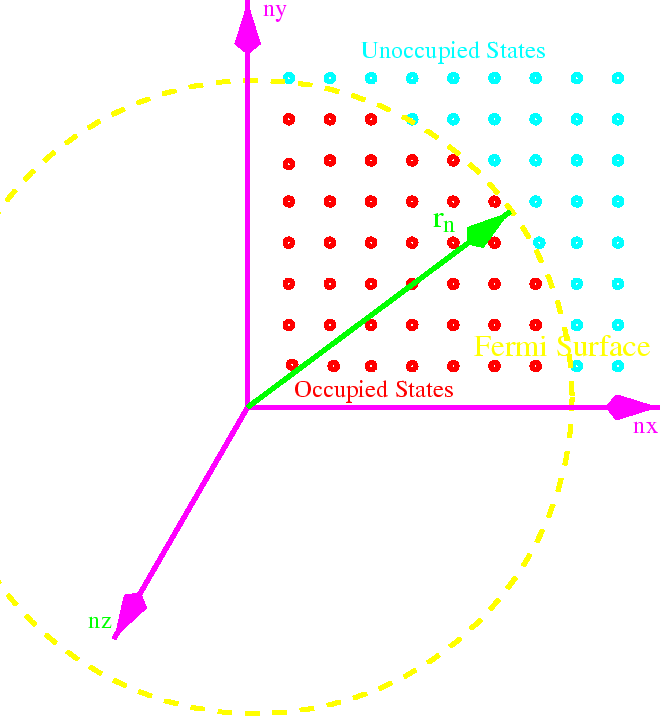
The number of states within the radius is
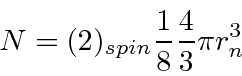
We can now relate the Fermi energy to the number of particles in the box.
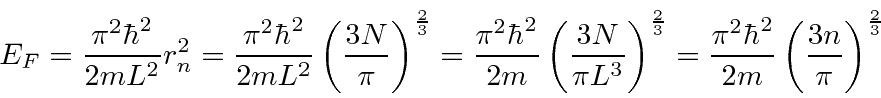
We can also integrate to get the total energy of all the fermions.
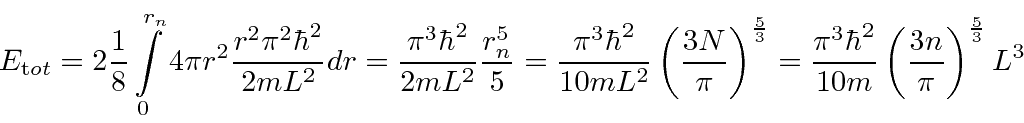
The step in which
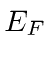 and
and
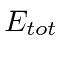 is related to
is related to
![]() is often useful.
is often useful.
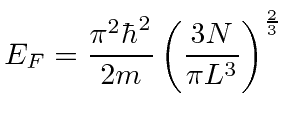
|
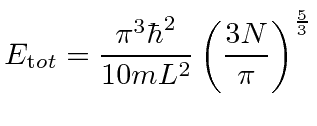 |
Jim Branson 2013-04-22