Particle in a 3D Box

An example of a problem which has a Hamiltonian of the separable form is the particle in a 3D box. The potential is zero inside the cube of side $L$and infinite outside. It can be written as a sum of terms.

$$\bgroup\color{black} H=H_x+H_y+H_z \egroup$$

The energies are

$$\bgroup\color{black} E_{nx,ny,nz}={\pi^2\hbar^2\over 2mL^2}(n_x^2+n_y^2+n_z^2) .\egroup$$

They depend on three quantum numbers, (since there are 3 degrees of freedom).

$$\bgroup\color{black} u_{nx,ny,nz}(\vec{r})=\sin\left({n_x\pi ... ...\pi y\over L}\right) \sin\left({n_z\pi z\over L}\right) \egroup$$

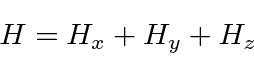
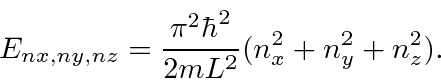
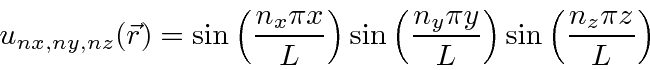
For a cubic box like this one, there will often be degenerate states.