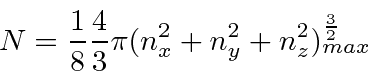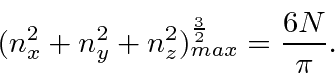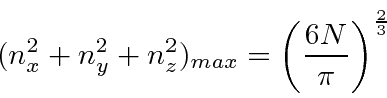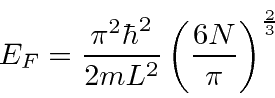- *
Calculate the Fermi energy for
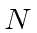 particles of mass
particles of mass 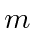 in a 3D cubic ``box'' of side
in a 3D cubic ``box'' of side 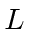 .
Ignore spin for this problem.
.
Ignore spin for this problem.
Answer
The energy levels are given in terms of three quantum numbers.
The number of states with inside some
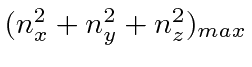 (
(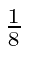 of a a sphere in
of a a sphere in 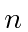 space) is
space) is
So for 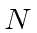 particles filling the levels,
particles filling the levels,
The energy corresponding to this is the Fermi energy.
- *
We put
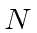 fermions of mass
fermions of mass 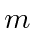 into a (cold) one dimensional box of length
into a (cold) one dimensional box of length 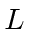 .
The particles go into the lowest energy states possible.
If the Fermi energy is defined as the energy of the highest energy particle,
what is the Fermi energy of this system?
You may assume that there are 2 spin states for these fermions.
.
The particles go into the lowest energy states possible.
If the Fermi energy is defined as the energy of the highest energy particle,
what is the Fermi energy of this system?
You may assume that there are 2 spin states for these fermions.
Jim Branson
2013-04-22
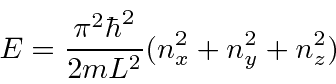
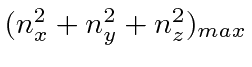 (
(