Next: Sample Test Problems Up: Extending QM to Two Previous: Two Particles in Three Contents
It is not possible to tell the difference between two electrons. They are identical in every way. Hence, there is a clear symmetry in nature under the interchange of any two electrons.
We define the interchange operator
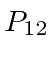 .
By our symmetry, this operator commutes with
.
By our symmetry, this operator commutes with
![]() so we can have simultaneous
eigenfunctions of energy and interchange.
so we can have simultaneous
eigenfunctions of energy and interchange.
If we interchange twice, we get back to the original state,
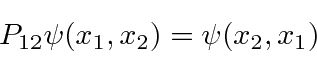
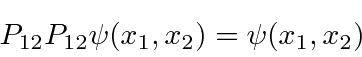

It turns out that both possibilities exist in nature. Some particles like the electron, always have the -1 quantum number. The are spin one-half particles and are called fermions. The overall wavefunction changes sign whenever we interchange any pair of fermions. Some particles, like the photon, always have the +1 quantum number. They are integer spin particles, called bosons.
There is an important distinction between fermions and bosons which we can
derive from the interchange symmetry.
If any two fermions are in the same state, the wave function must be zero
in order to be odd under interchange.
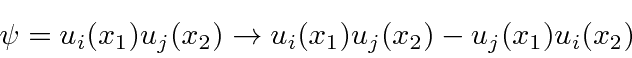
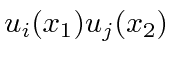 when what we mean is the
antisymmetrized version of that state
when what we mean is the
antisymmetrized version of that state
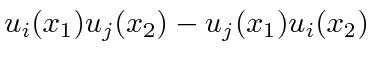 .)
Thus, no two fermions can be in the same state.
This is often called the Pauli exclusion principle.
.)
Thus, no two fermions can be in the same state.
This is often called the Pauli exclusion principle.
In fact, the interchange symmetry difference makes fermions behave like matter and bosons behave like energy. The fact that no two fermions can be in the same state means they take up space, unlike bosons. It is also related to the fact that fermions can only be created in conjunction with anti-fermions. They must be made in pairs. Bosons can be made singly and are their own anti-particle as can be seen from any light.
Jim Branson 2013-04-22