Two Particles in Three Dimensions

The generalization of the Hamiltonian to three dimensions is simple.

$$\bgroup\color{black}H={\vec{p}_1^2\over 2m}+{\vec{p}_2^2\over 2m}+V(\vec{r}_1-\vec{r}_2)\egroup$$

We define the vector difference between the coordinates of the particles.

$$\vec{r}\equiv\vec{r}_1-\vec{r}_2$$

We also define the vector position of the center of mass.

$$\vec{R}\equiv{m_1\vec{r}_1+m_2\vec{r}_2\over m_1+m_2}$$

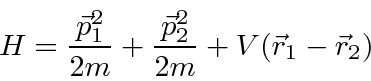
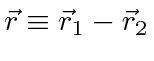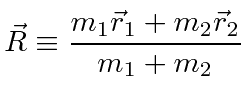We will use the chain rule to transform our Hamiltonian. As a simple example, if we were working in one dimension we might use the chain rule like this.

$$\bgroup\color{black}{d\over dr_1}={\partial r\over\partial r_... ...+{\partial R\over\partial r_1}{\partial\over\partial R} \egroup$$

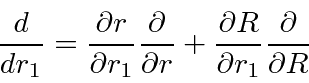
In three dimensions we would have.

$$\bgroup\color{black}\vec{\nabla}_1=\vec{\nabla}_r+{m_1\over m_1+m_2}\vec{\nabla}_R \egroup$$

$$\bgroup\color{black}\vec{\nabla}_2=-\vec{\nabla}_r+{m_2\over m_1+m_2}\vec{\nabla}_R \egroup$$

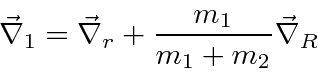
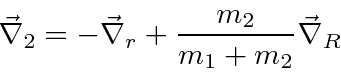
Putting this into the Hamiltonian we get

$$\bgroup\color{black}H={-\hbar^2\over 2m_1}\left[\vec{\nabla}_... ...1\over m_1+m_2}\vec{\nabla}_r\cdot\vec{\nabla}_R\right] \egroup$$

$$\bgroup\color{black}\qquad +{-\hbar^2\over 2m_2}\left[\vec{\n... ...m_2}\vec{\nabla}_r\cdot\vec{\nabla}_R\right]+V(\vec{r}) \egroup$$

$$\bgroup\color{black}H=-\hbar^2\left[ \left({1\over 2m_1}+{1\o... ...over 2(m_1+m_2)^2}\vec{\nabla}_R^2\right]+V(\vec{r}) . \egroup$$

Defining the reduced mass $\mu$

$${1\over\mu}={1\over m_1}+{1\over m_2}$$

and the total mass

$$M=m_1+m_2$$

we get.

$$H=-{\hbar^2\over 2\mu}\vec{\nabla}_r^2-{\hbar^2\over 2M}\vec{\nabla}_R^2+V(\vec{r})$$

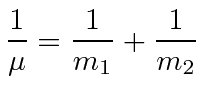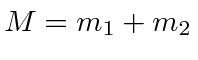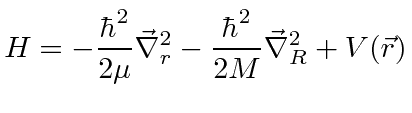The Hamiltonian actually separates into two problems: the motion of the center of mass as a free particle

$$\bgroup\color{black}H={-\hbar^2\over 2M}\vec{\nabla}_R^2\egroup$$

and the interaction between the two particles.

$$H=-{\hbar^2\over 2\mu}\vec{\nabla}_r^2+V(\vec{r})$$

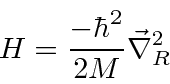
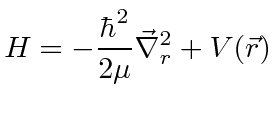This is exactly the same separation that we would make in classical physics.