Quantum Mechanics in Three Dimensions

We have generalized Quantum Mechanics to include more than one particle. We now wish to include more than one dimension too.

Additional dimensions are essentially independent although they may be coupled through the potential. The coordinates and momenta from different dimensions commute. The fact that the commutators are zero can be calculated from the operators that we know. For example,

$$\bgroup\color{black} [x,p_y]=[x,{\hbar\over i}{\partial\over\partial y}] =0 .\egroup$$

The kinetic energy can simply be added and the potential now depends on 3 coordinates. The Hamiltonian in 3D is

$$\bgroup\color{black} H={p_x^2\over 2m}+{p_y^2\over 2m}+{p_z^2... ...r 2m}+V(\vec{r})=-{\hbar^2\over 2m}\nabla^2+V(\vec{r}) .\egroup$$

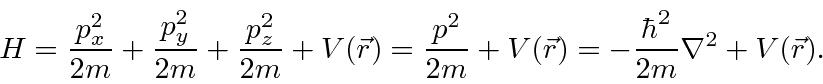
This extension is really very simple.