We can know the state of two particles at the same time.
The positions and momenta of particle 2 commute with the positions and momenta of particle 1.
The kinetic energy terms in the Hamiltonian are independent.
There may be an interaction between the two particles in the potential.
The Hamiltonian for two particles can be easily written.
Often, the potential will only depend on the
difference in the positions of the two particles.
This means that the overall Hamiltonian has a translational symmetry.
Lets examine an infinitesimal translation in
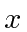 .
The original Schrödinger equation
.
The original Schrödinger equation
transforms to
which can be Taylor expanded
We can write the derivatives in terms of the total momentum operator.
Subtract of the initial Schrödinger equation and commute
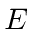 through
through
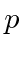 .
.
We have proven that
if the Hamiltonian has translational symmetry.
The momentum is a constant of the motion.
Momentum is conserved.
We can have simultaneous eigenfunctions of the total momentum and of energy.
Jim Branson
2013-04-22
![\begin{displaymath}\bgroup\color{black} [x_1,x_2]=[p_1,p_2]=[x_1,p_2]=[x_2,p_1]=0 \egroup\end{displaymath}](img1583.png)
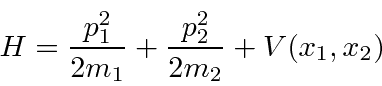
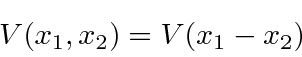
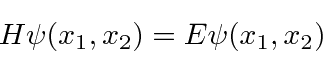
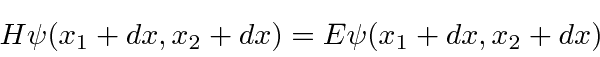
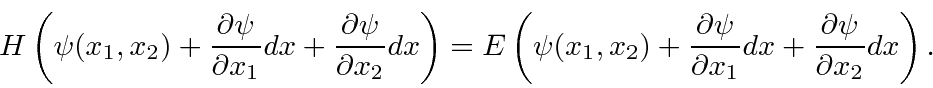
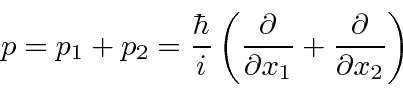
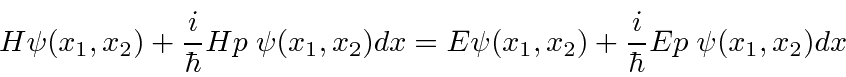
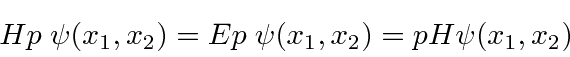
![\begin{displaymath}\bgroup\color{black}[H,p]=0 \egroup\end{displaymath}](img1592.png)