- A Hydrogen atom is in its 4D state
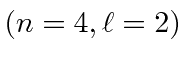 .
The atom decays to a lower state by emitting a photon.
Find the possible photon energies that may be observed. Give your answers in eV.
.
The atom decays to a lower state by emitting a photon.
Find the possible photon energies that may be observed. Give your answers in eV.
Answer
The 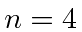 state can decay into states with
state can decay into states with 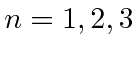 .
(Really the
.
(Really the 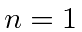 state will be suppressed due to selection rules but this is supposed to be a simple question.)
The energies of the states are
state will be suppressed due to selection rules but this is supposed to be a simple question.)
The energies of the states are
The photon energy is given by the energy difference between the states.
For the 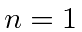 final state,
final state,
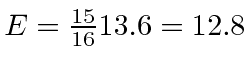 eV.
eV.
For the 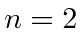 final state,
final state,
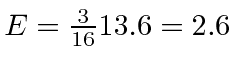 eV.
eV.
For the 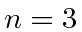 final state,
final state,
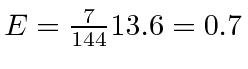 eV.
eV.
- Using the
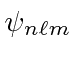 notation, list all the
notation, list all the 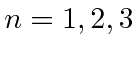 hydrogen states.
(Neglect the existence of spin.)
hydrogen states.
(Neglect the existence of spin.)
Answer
The states are, 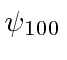 ,
, 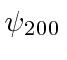 ,
, 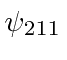 ,
, 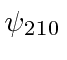 ,
, 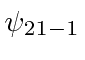 ,
, 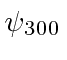 ,
, 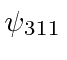 ,
,
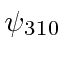 ,
, 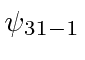 ,
, 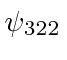 ,
, 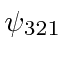 ,
, 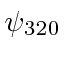 ,
, 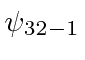 ,
, 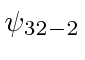 .
.
- Find the difference in wavelength between light emitted from the
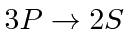 transition in Hydrogen and light from the same transition
in Deuterium. (Deuterium is an isotope of Hydrogen with a proton and a neutron
in the nucleus.)
Get a numerical answer.
transition in Hydrogen and light from the same transition
in Deuterium. (Deuterium is an isotope of Hydrogen with a proton and a neutron
in the nucleus.)
Get a numerical answer.
- An electron in the Coulomb field of a proton is in the state described by the wave function
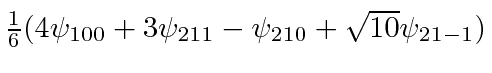 .
Find the expected value of the Energy,
.
Find the expected value of the Energy, 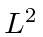 and
and 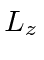 .
Now find the expected value of
.
Now find the expected value of 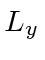 .
.
- *
Write out the (normalized) hydrogen energy eigenstate
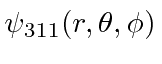 .
.
- Calculate the expected value of
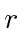 in the Hydrogen state
in the Hydrogen state 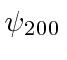 .
.
- Write down the wave function of the hydrogen atom state
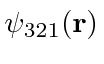 .
.
- A Hydrogen atom is in its
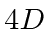 state
state 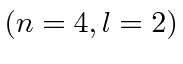 . The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in
. The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in 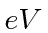 .
.
- A Hydrogen atom is in the state:
For the Hydrogen eigenstates,
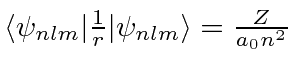 .
Find the expected value of the potential energy for this state.
Find the expected value of
.
Find the expected value of the potential energy for this state.
Find the expected value of 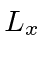 .
.
- A Hydrogen atom is in its
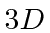 state
state 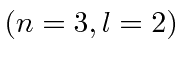 . The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in
. The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in 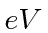 .
.
- The hydrogen atom is made up of a proton and an electron bound together
by the Coulomb force. The electron has a mass of 0.51 MeV/
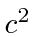 . It is
possible to make a hydrogen-like atom from a proton and a muon. The force
binding the muon to the proton is identical to that for the electron but
the muon has a mass of 106 MeV/
. It is
possible to make a hydrogen-like atom from a proton and a muon. The force
binding the muon to the proton is identical to that for the electron but
the muon has a mass of 106 MeV/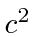 .
.
- a)
- What is the ground state energy of muonic hydrogen (in eV).
- b)
- What is the``Bohr Radius'' of the ground state
of muonic hydrogen.
- A hydrogen atom is in the state:
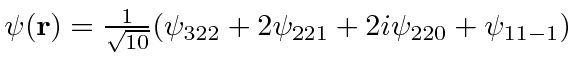 Find the possible measured energies and the probabilities of each.
Find the expected value of
Find the possible measured energies and the probabilities of each.
Find the expected value of 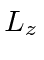 .
.
- Find the difference in frequency between light emitted from the
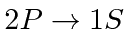 transition in Hydrogen and light from the same transition
in Deuterium. (Deuterium is an isotope of Hydrogen with a proton and a neutron
in the nucleus.)
transition in Hydrogen and light from the same transition
in Deuterium. (Deuterium is an isotope of Hydrogen with a proton and a neutron
in the nucleus.)
- Tritium is an isotope of hydrogen having 1 proton and 2 neutrons in the
nucleus. The nucleus is unstable and decays by changing one of the neutrons
into a proton with the emission of a positron and a neutrino. The atomic
electron is undisturbed by this decay process and therefore finds itself
in exactly the same state immediately after the decay as before it.
If the electron started off in the
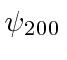 (
(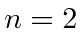 ,
, 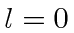 ) state of
tritium, compute the probability to find the electron in the ground state
of the new atom with Z=2.
) state of
tritium, compute the probability to find the electron in the ground state
of the new atom with Z=2.
- At
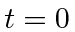 a hydrogen atom is in the state
a hydrogen atom is in the state
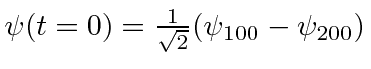 .
Calculate the expected value of
.
Calculate the expected value of 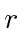 as a function of time.
as a function of time.
Answer
The angular part of the integral can be done. All the terms of the wavefunction contain a 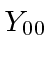 and
and 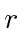 does not depend
on angles, so the angular integral just gives 1.
does not depend
on angles, so the angular integral just gives 1.
The cross terms are not zero because of the 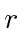 .
.
Now we will need to put in the actual radial wavefunctions.
Jim Branson
2013-04-22
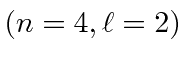 .
The atom decays to a lower state by emitting a photon.
Find the possible photon energies that may be observed. Give your answers in eV.
.
The atom decays to a lower state by emitting a photon.
Find the possible photon energies that may be observed. Give your answers in eV.
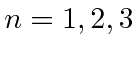 .
(Really the
.
(Really the 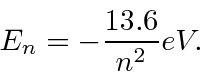
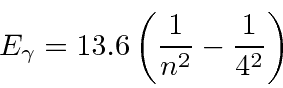
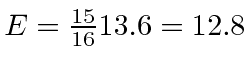 eV.
eV.
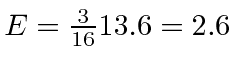 eV.
eV.
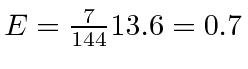 eV.
eV.
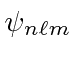 notation, list all the
notation, list all the 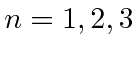 hydrogen states.
(Neglect the existence of spin.)
hydrogen states.
(Neglect the existence of spin.)
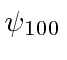 ,
, 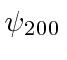 ,
, 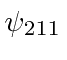 ,
, 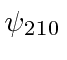 ,
, 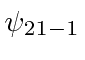 ,
, 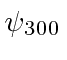 ,
, 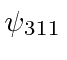 ,
,
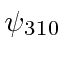 ,
, 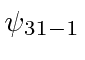 ,
, 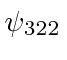 ,
, 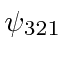 ,
, 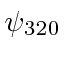 ,
, 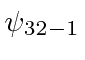 ,
, 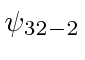 .
.
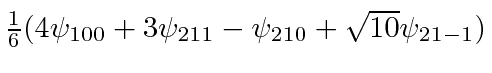 .
Find the expected value of the Energy,
.
Find the expected value of the Energy, 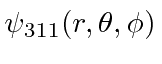 .
.
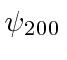 .
.
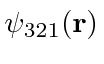 .
.
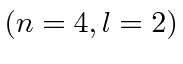 . The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in
. The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in 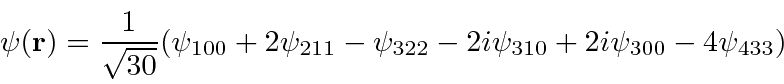
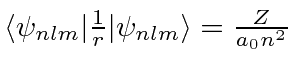 .
Find the expected value of the potential energy for this state.
Find the expected value of
.
Find the expected value of the potential energy for this state.
Find the expected value of 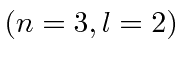 . The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in
. The atom
decays to a lower state by emitting a photon. Find the possible photon
energies that may be observed. Give your answers in 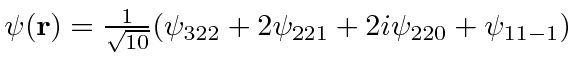 Find the possible measured energies and the probabilities of each.
Find the expected value of
Find the possible measured energies and the probabilities of each.
Find the expected value of 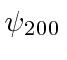 (
(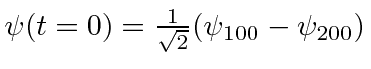 .
Calculate the expected value of
.
Calculate the expected value of 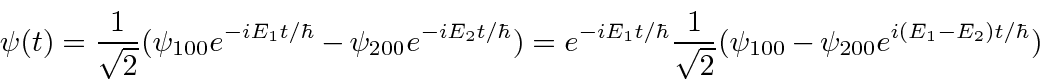
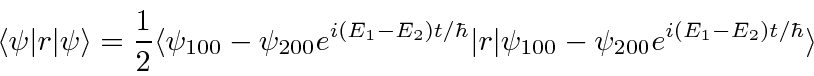
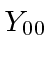 and
and 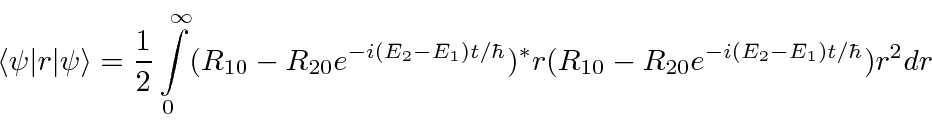
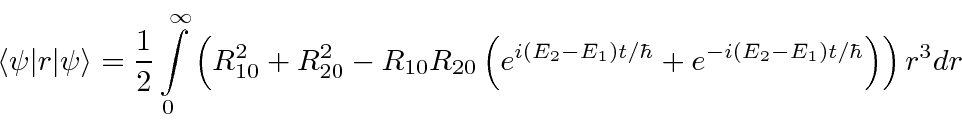
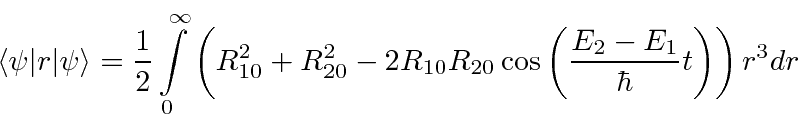
![\begin{eqnarray*}
R_{10}&=&2\left({1\over a_0}\right)^{3\over 2} e^{-r/a_0} \\
...
...rt{2}\over 81}
\cos\left({E_2-E_1\over\hbar}t\right) \right] \\
\end{eqnarray*}](img2074.png)