Hydrogen

The Hydrogen atom consists of an electron bound to a proton by the Coulomb potential.

$$\bgroup\color{black}V(r)=-{e^2\over r} \egroup$$

We can generalize the potential to a nucleus of charge $Ze$ without complication of the problem.

$$\bgroup\color{black}V(r)=-{Ze^2\over r} \egroup$$

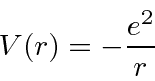
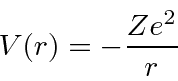
Since the potential is spherically symmetric, the problem separates and the solutions will be a product of a radial wavefunction and one of the spherical harmonics.

$$\bgroup\color{black}\psi_{n\ell m}(\vec{r})=R_{n\ell}(r)Y_{\ell m}(\theta,\phi) \egroup$$

We have already studied the spherical harmonics.

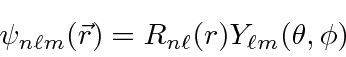
The radial wavefunction satisfies the differential equation that depends on the angular momentum quantum number $\ell$,

$$\bgroup\color{black}\left({d^2\over dr^2}+{2\over r}{d\over d... ...\ell(\ell+1)\hbar^2\over 2\mu r^2}\right)R_{E\ell}(r)=0 \egroup$$

where $\mu$ is the reduced mass of the nucleus and electron.

$$\bgroup\color{black} \mu={m_em_N\over m_e+m_N} \egroup$$

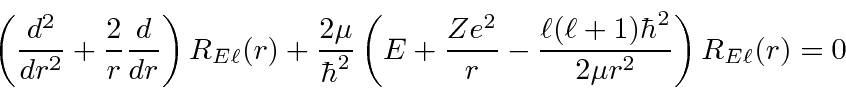
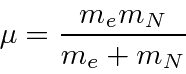
The differential equation can be solved using techniques similar to those used to solve the 1D harmonic oscillator equation. We find the eigen-energies

$$E=-{1\over 2n^2}Z^2\alpha^2\mu c^2$$

and the radial wavefunctions

$$R_{n\ell}(\rho)=\rho^\ell\sum\limits_{k=0}^\infty a_k\rho^k e^{-\rho/2}$$

where the coefficients of the polynomials can be found from the recursion relation

$$a_{k+1}={k+\ell+1-n\over (k+1)(k+2\ell+2)}a_k$$

and

$$\rho=\sqrt{-8\mu E\over\hbar^2}r .$$

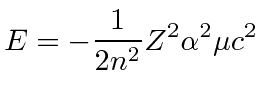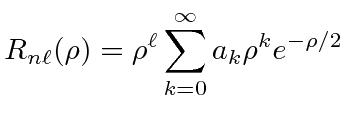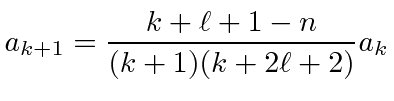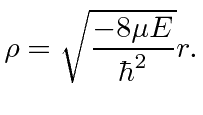The principle quantum number $n$ is an integer from 1 to infinity.

$$\bgroup\color{black} n=1,2,3,... \egroup$$

This principle quantum number is actually the sum of the radial quantum number plus $\ell$ plus 1.

$$\bgroup\color{black}n=n_r+\ell+1\egroup$$

and therefore, the total angular momentum quantum number $\ell$ must be less than $n$.

$$\bgroup\color{black} \ell=0,1,2,...,n-1 \egroup$$

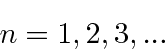
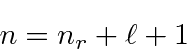
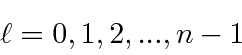
This unusual way of labeling the states comes about because a radial excitation has the same energy as an angular excitation for Hydrogen. This is often referred to as an accidental degeneracy.