Next: The Hydrogen Spectrum Up: Hydrogen Previous: Hydrogen Contents
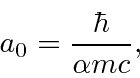
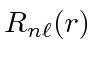 .
.
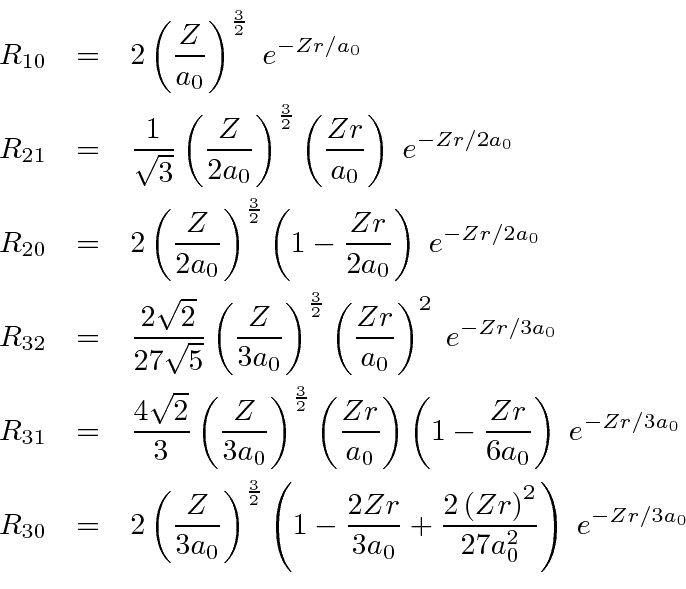
For a given principle quantum number
![]() ,the largest
,the largest
![]() radial wavefunction is given by
radial wavefunction is given by
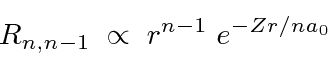
The radial wavefunctions should be normalized as below.
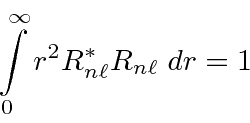
* Example:
Compute the expected values of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() in the Hydrogen state
in the Hydrogen state
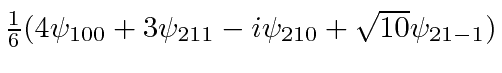 .*
.*
The pictures below depict the probability distributions in space for the Hydrogen wavefunctions.
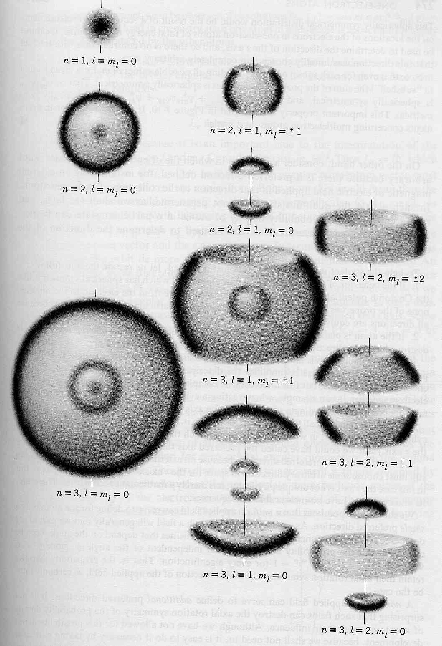
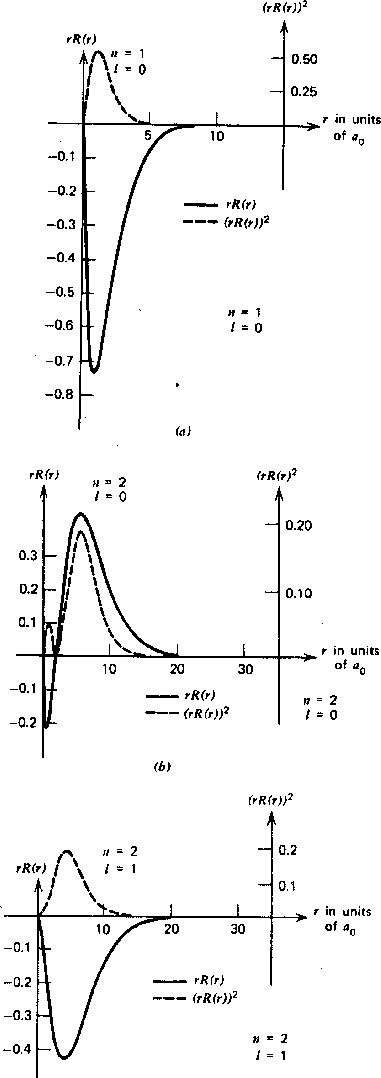
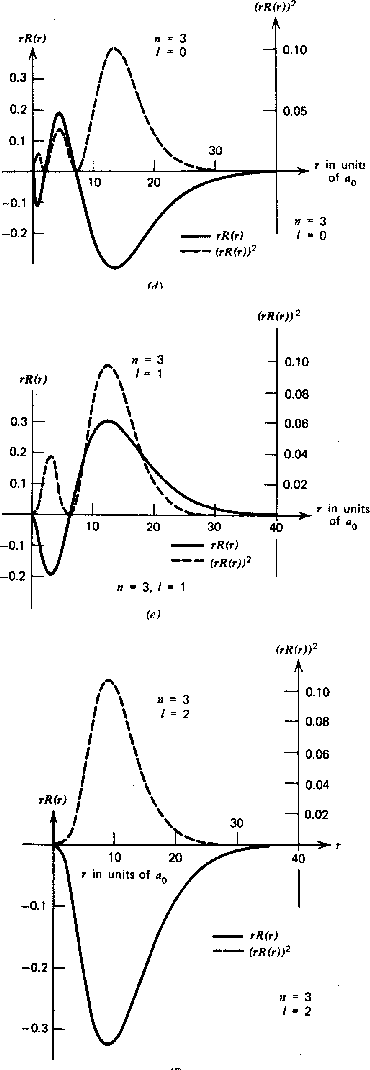
The graphs below show the radial wave functions.
Again, for a given
![]() the maximum
the maximum
![]() state has no radial excitation, and hence no nodes in the radial wavefunction.
As
state has no radial excitation, and hence no nodes in the radial wavefunction.
As
![]() gets smaller for a fixed
gets smaller for a fixed
![]() , we see more radial excitation.
, we see more radial excitation.
A useful integral for Hydrogen atom calculations is.
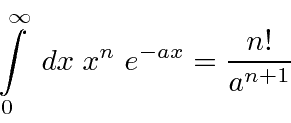
* Example:
What is the expectation value of ![]() in the state
in the state 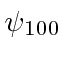 ?*
?*
* Example:
What is the expectation value of ![]() in the state
in the state 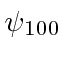 ?*
?*
* Example:
What is the expectation value of the radial component of velocity in the state 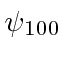 ?*
?*
Jim Branson 2013-04-22