Next: Computing the Radial Wavefunctions Up: Derivations and Calculations Previous: Derivations and Calculations Contents
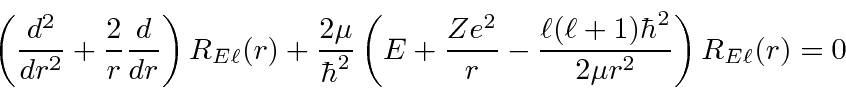
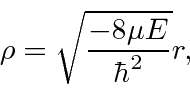
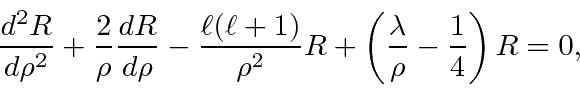
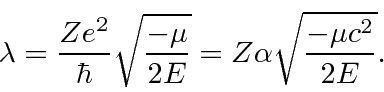
Next we look at the equation for large
![]() .
.
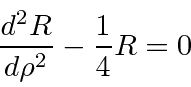
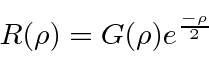
We should also pick of the small
![]() behavior.
behavior.
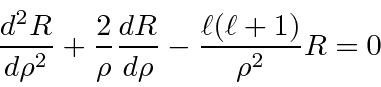
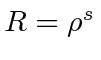 , we get
, we get
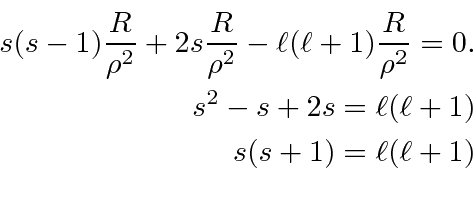
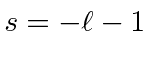 .
The second is not well normalizable.
We write
.
The second is not well normalizable.
We write 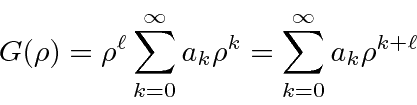
The differential equation for
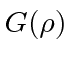 is
is
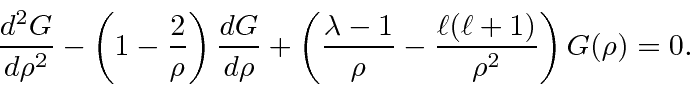
We plug the sum into the differential equation.
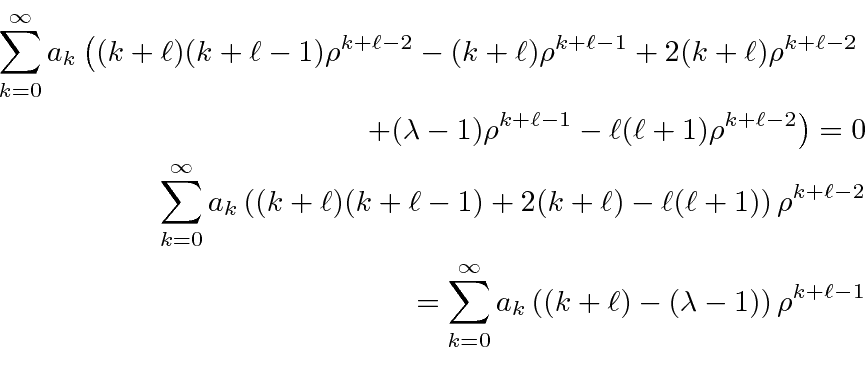
Now we shift the sum so that each term contains
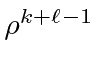 .
.
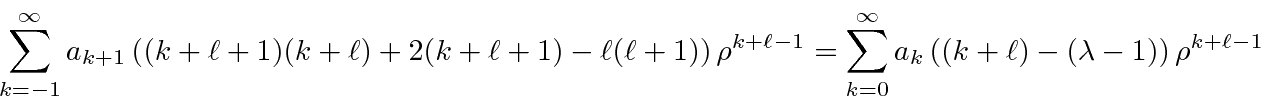
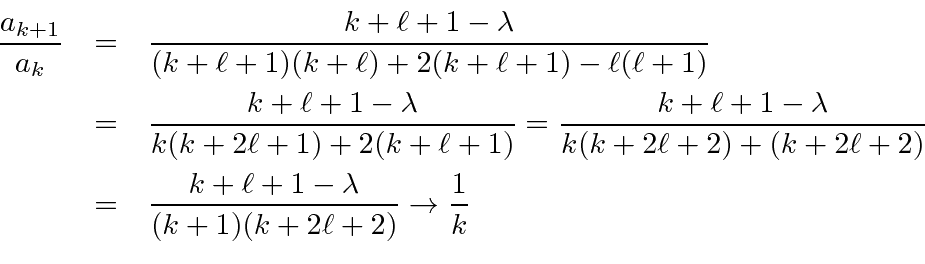
This is then the power series for
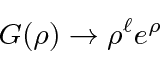
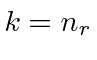 ,
,
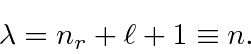
Plugging in for
![]() we get the energy eigenvalues.
we get the energy eigenvalues.
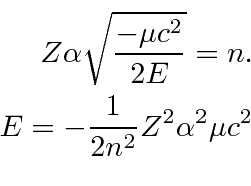
The solutions are
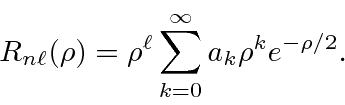
The recursion relation is
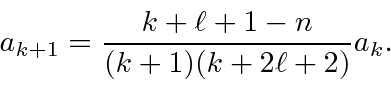
We can rewrite
![]() , substituting the energy eigenvalue.
, substituting the energy eigenvalue.
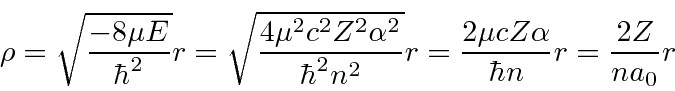
Jim Branson 2013-04-22