- A particle has orbital angular momentum quantum number
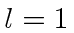 and
is bound in the potential well
and
is bound in the potential well
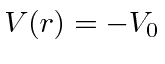 for
for 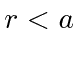 and
and 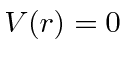 elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at
elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at 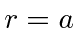 to get one
equation, the solution of which will quantize the
energies. Do not bother to solve the equation.
to get one
equation, the solution of which will quantize the
energies. Do not bother to solve the equation.
- A particle of mass
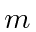 with 0 total angular momentum is in a 3 dimensional potential well
with 0 total angular momentum is in a 3 dimensional potential well
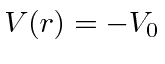 for
for 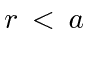 (otherwise
(otherwise 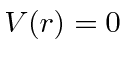 ).
).
- a)
- Write down the form of the (
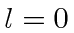 ) solution, to the time independent
Schrödinger equation, inside the well, which is well behaved at
at
) solution, to the time independent
Schrödinger equation, inside the well, which is well behaved at
at 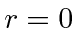 . Specify the relationship between the particles energy and
any parameters in your solution.
. Specify the relationship between the particles energy and
any parameters in your solution.
- b)
- Write down the form of the solution to the time independent
Schrödinger equation, outside the well, which has the right
behavior as
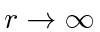 . Again specify how the parameters depend
on energy.
. Again specify how the parameters depend
on energy.
- c)
- Write down the boundary conditions that must be satisfied to
match the two regions. Use
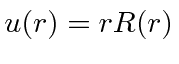 to simplify the calculation.
to simplify the calculation.
- d)
- Find the transcendental equation which will determine the
energy eigenvalues.
- A particle has orbital angular momentum quantum number
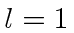 and
is bound in the potential well
and
is bound in the potential well
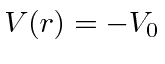 for
for 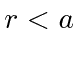 and
and 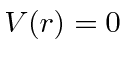 elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at
elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at 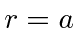 to get one
equation, the solution of which will quantize the
energies. Do not bother to solve the equation.
to get one
equation, the solution of which will quantize the
energies. Do not bother to solve the equation.
- A particle is confined to the inside of a sphere of radius
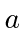 .
Find the energies of the two lowest energy states for
.
Find the energies of the two lowest energy states for 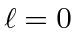 .
Write down (but do not solve) the equation for the energies for
.
Write down (but do not solve) the equation for the energies for 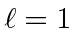 .
.
Jim Branson
2013-04-22
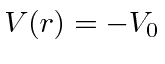 for
for 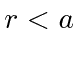 and
and 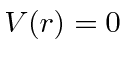 elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at
elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at 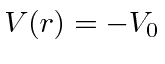 for
for 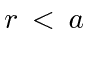 (otherwise
(otherwise 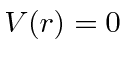 ).
).
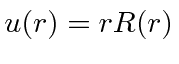 to simplify the calculation.
to simplify the calculation.
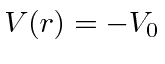 for
for 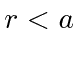 and
and 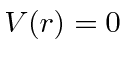 elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at
elsewhere.
Write down the form of the solution (in terms of known
functions) in the two regions.
Your solution should satisfy constraints at the origin
and at infinity.
Be sure to include angular dependence.
Now use the boundary condition at